题目内容
【题目】已知函
数是奇函数，且f(2)＝
.
(1)求实数m和n的值；
(2)求函数f(x)在区间[－2，－1]上的最值．
【答案】（1）实数m和n的值分别是2和0；（2）
.
【解析】试题分析: 已知函数的奇偶性求函数的解析式是函数的奇偶性常见考试题，由于函数是奇函数，则
，又f(2)= 
，列方程组解出m，n，求出函数的解析式，有了函数的解析式可以利用定义研究函数的单调性，也可借助对勾函数研究函数的单调性，也可借助导数研究函数的单调性，进而求函数在某区间上的最值.
试题解析：
(1)∵f(x)是奇函数，∴f(－x)＝－f(x)，
∴
.
比较得n＝－n，n＝0.
又f(2)＝
，∴
，解得m＝2.
因此，实数m和n的值分别是2和0.
(2)由(1)知f(x)＝
.
任取x1，x2∈[－2，－1]，且x1＜x2，
则f(x1)－f(x2)＝
(x1－x2)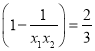 
(x1－x2)·
.
∵－2≤x1＜x2≤－1时，
∴x1－x2＜0，x1x2＞0，x1x2－1＞0，
∴f(x1)－f(x2)＜0，即f(x1)＜f(x2)．
∴函数f(x)在[－2，－1]上为增函数，
因此f(x)max＝f(－1)＝－
，f(x)min＝f(－2)＝－
.
练习册系列答案
相关题目
【题目】某出租车公司为了解本公司出租车司机对新法规的知晓情况，随机对
名出租车司机进行调查，调查问卷共
道题，答题情况如下表：
答对题目数 |
|
|
|
|
女 |
|
|
|
|
男 |
|
|
|
|
（I）如果出租车司机答对题目大于等于
，就认为该司机对新法规的知晓情况比较好，试估计该公司的出租车司机对新法规知晓情况比较好的概率；
（II）从答对题目数小于
的出租车司机中选出
人做进一步的调查，求选出的人中至少有一名女出租车司机的概率.
