题目内容
(类型A)已知数列{an}的前项和为Sn,a1=-
,满足Sn+
+2=an(n≥2),计算S1,S2,S3,S4,猜想Sn的表达式并用数学归纳法加以证明
(类型B)已知数列{an}的前项和为Sn,a1=-
,满足Sn=-
(n≥2),计算S1,S2,S3,S4,猜想Sn的表达式并用数学归纳法加以证明.
| 2 |
| 3 |
| 1 |
| Sn |
(类型B)已知数列{an}的前项和为Sn,a1=-
| 2 |
| 3 |
| 1 |
| Sn-1+2 |
(类型B)∵S1= a1=-
∴S2=-
= -
,S3=-
=-
,S4=-
=-
猜想:Sn=-
(2)假设当n=k时成立,即Sk=-
当n=k+1时,Sk+1=-
=-
=-
=-
对n=k+1时成立
综上可得对任意n∈N*都成立,猜想正确
| 2 |
| 3 |
∴S2=-
| 1 |
| S1+2 |
| 3 |
| 4 |
| 1 |
| S2+2 |
| 4 |
| 5 |
| 1 |
| S3+2 |
| 5 |
| 6 |
猜想:Sn=-
| n+1 |
| n+2 |
(2)假设当n=k时成立,即Sk=-
| k+1 |
| k+2 |
当n=k+1时,Sk+1=-
| 1 |
| Sk+2 |
| 1 | ||
-
|
| k+2 |
| k+3 |
| (k+1)+1 |
| (k+1)+2 |
综上可得对任意n∈N*都成立,猜想正确

练习册系列答案
相关题目
 ,满足
,满足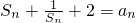 (n≥2),计算S1,S2,S3,S4,猜想Sn的表达式并用数学归纳法加以证明
(n≥2),计算S1,S2,S3,S4,猜想Sn的表达式并用数学归纳法加以证明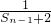 (n≥2),计算S1,S2,S3,S4,猜想Sn的表达式并用数学归纳法加以证明.
(n≥2),计算S1,S2,S3,S4,猜想Sn的表达式并用数学归纳法加以证明. ,满足
,满足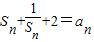 (n≥2),计算S1,S2,S3,S4,猜想Sn的表达式并用数学归纳法加以证明
(n≥2),计算S1,S2,S3,S4,猜想Sn的表达式并用数学归纳法加以证明 ,满足Sn=-
,满足Sn=-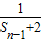 (n≥2),计算S1,S2,S3,S4,猜想Sn的表达式并用数学归纳法加以证明.
(n≥2),计算S1,S2,S3,S4,猜想Sn的表达式并用数学归纳法加以证明.