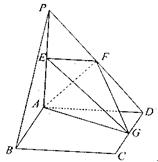
题目内容
如图所示，平面PAD⊥平面ABCD，ABCD为正方形，PA⊥AD，且PA=AD=2，E，F，G分别是线段PA，PD，CD的中点．
（1）求证：BC∥平面EFG；
（2）求三棱锥E﹣AFG的体积．
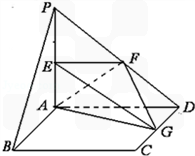
（1）求证：BC∥平面EFG；
（2）求三棱锥E﹣AFG的体积．
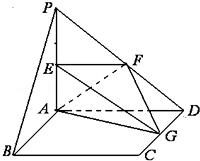
（1）证明：∵E，F分别是线段PA、PD的中点，
∴EF∥AD．
又∵ABCD为正方形，
∴BC∥AD，
∴BC∥EF．
又∵BC
平面EFG，EF
平面EFG，
∴BC∥平面EFG
（2）解：∵平面PAD⊥平面ABCD，CD⊥AD，
∴CD⊥平面PAD，即GD⊥平面AEF．
又∵EF∥AD，PA⊥AD，
∴EF⊥AE．
又∵
，
∴
=
．
∴EF∥AD．
又∵ABCD为正方形，
∴BC∥AD，
∴BC∥EF．
又∵BC
平面EFG，EF平面EFG， ∴BC∥平面EFG
（2）解：∵平面PAD⊥平面ABCD，CD⊥AD，
∴CD⊥平面PAD，即GD⊥平面AEF．
又∵EF∥AD，PA⊥AD，
∴EF⊥AE．
又∵
，∴
=．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
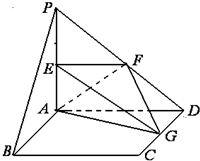如图所示，平面PAD⊥平面ABCD，ABCD为正方形，PA⊥AD，且PA=AD=2，E，F，G分别是线段PA，PD，CD的中点．
