题目内容
已知数列{an}中, ,且当
,且当 时,函数
时,函数 取得极值.
取得极值.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)数列{bn}满足:b1=2, ,证明:
,证明: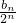 是等差数列,并求数列{bn}的通项公式通项及前n项和Sn.
是等差数列,并求数列{bn}的通项公式通项及前n项和Sn.
解:(Ⅰ)f′(x)=an•x-an+1
由题意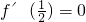 得
得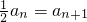
∴数列{an}是首项为 ,公比为
,公比为 的等比数列,∴
的等比数列,∴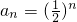
(Ⅱ)由(1)知bn+1-2bn=2n+1,∴bn+1=2bn+2n+1
∴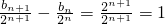
∴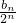 是以1为首项,1位公差的等差数列
是以1为首项,1位公差的等差数列
∴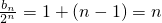 ,∴bn=n•2n
,∴bn=n•2n
Sn=1•2+2•22++n•2n,2Sn=1•22++(n-1)•2n+n•2n+1
两式相减得:-Sn=2+22++2n-n•2n+1=(1-n)•2n+1-2
∴Sn=(n-1)•2n+1+2
分析:(I)由当 时,函数
时,函数 取得极值,先求出函数
取得极值,先求出函数 的导数,得
的导数,得
f′(x)=an•x-an+1,再由x=2时,导数为0得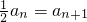 ,进而用等比数列的通项公式去求.
,进而用等比数列的通项公式去求.
(Ⅱ)可通过证明数列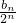 的后一项减前一项是同一常数,来证明明数列
的后一项减前一项是同一常数,来证明明数列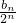 是等差数列.再用错位相减法求和.
是等差数列.再用错位相减法求和.
点评:此题主要考查了数列通项公式的求法,以及错位相减法求数列和,做题时要认真审题,发现规律.
由题意
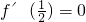 得
得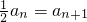
∴数列{an}是首项为
 ,公比为
,公比为 的等比数列,∴
的等比数列,∴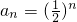
(Ⅱ)由(1)知bn+1-2bn=2n+1,∴bn+1=2bn+2n+1
∴
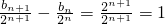
∴
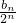 是以1为首项,1位公差的等差数列
是以1为首项,1位公差的等差数列∴
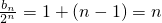 ,∴bn=n•2n
,∴bn=n•2nSn=1•2+2•22++n•2n,2Sn=1•22++(n-1)•2n+n•2n+1
两式相减得:-Sn=2+22++2n-n•2n+1=(1-n)•2n+1-2
∴Sn=(n-1)•2n+1+2
分析:(I)由当
 时,函数
时,函数 取得极值,先求出函数
取得极值,先求出函数 的导数,得
的导数,得f′(x)=an•x-an+1,再由x=2时,导数为0得
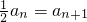 ,进而用等比数列的通项公式去求.
,进而用等比数列的通项公式去求.(Ⅱ)可通过证明数列
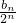 的后一项减前一项是同一常数,来证明明数列
的后一项减前一项是同一常数,来证明明数列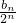 是等差数列.再用错位相减法求和.
是等差数列.再用错位相减法求和.点评:此题主要考查了数列通项公式的求法,以及错位相减法求数列和,做题时要认真审题,发现规律.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知数列{an}中,a1=1,2nan+1=(n+1)an,则数列{an}的通项公式为( )
A、
| ||
B、
| ||
C、
| ||
D、
|