题目内容
计算:
(1)lg20+lg5-log2
-log327;
(2)2
×
×
.
(1)lg20+lg5-log2
| 1 |
| 2 |
(2)2
| 3 |
| 6 | 12 |
| 3 |
| ||
分析:(1)直接利用对数的运算性质求得lg20+lg5-log2
-log327的值.
(2)利用根式与分数指数幂的互化,分数指数幂的运算性质求得2
×
×
的值.
| 1 |
| 2 |
(2)利用根式与分数指数幂的互化,分数指数幂的运算性质求得2
| 3 |
| 6 | 12 |
| 3 |
| ||
解答:解:(1)lg20+lg5-log2
-log327=lg(20×5)-log22-1-log333=2+1-3=0
(2)2
×
×
=2×3
×12
×(
)
=21+
-
×3
+
+
=2×3=6
| 1 |
| 2 |
(2)2
| 3 |
| 6 | 12 |
| 3 |
| ||
| 1 |
| 2 |
| 1 |
| 6 |
| 3 |
| 2 |
| 1 |
| 3 |
| 2 |
| 6 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 3 |
点评:本题主要考查根式与分数指数幂的互化,分数指数幂的运算性质、以及对数的运算性质的应用,属于基础题.

练习册系列答案
相关题目
 +
+ +lg20-lg2-(log32)•(log23)
+lg20-lg2-(log32)•(log23) -
- -lg
-lg -sin30°+(
-sin30°+( -1)lg1.
-1)lg1. +
+ +lg20-lg2-(log32)•(log23)
+lg20-lg2-(log32)•(log23) -
- -lg
-lg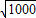 -sin30°+(
-sin30°+( -1)lg1.
-1)lg1. +
+ +lg20-lg2-(log32)•(log23)
+lg20-lg2-(log32)•(log23) -
- -lg
-lg -sin30°+(
-sin30°+( -1)lg1.
-1)lg1.