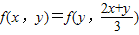题目内容
已知二元函数f(x,y)满足下列关系:
①f(x,x)=x
②f(kx,ky)=kf(x,y)(k为非零常数)
③f(x1,y1)+f(x2,y2)=f(x1+x2,y1+y2)
④
则f(x,y)关于x,y的解析式为f(x,y)=________.

分析:由已知中二元函数f(x,y)满足下列关系:①f(x,x)=x,②f(kx,ky)=kf(x,y)(k为非零常数),③f(x1,y1)+f(x2,y2)=f(x1+x2,y1+y2),④
 ,我们可以设f(1,0)=a,f(0,1)=b,由③得:f(x,y)=ax+by,由②、④构造关于a,b的方程组,解方程组求出a,b的值,即可求出f(x,y)关于x,y的解析式.
,我们可以设f(1,0)=a,f(0,1)=b,由③得:f(x,y)=ax+by,由②、④构造关于a,b的方程组,解方程组求出a,b的值,即可求出f(x,y)关于x,y的解析式.解答:设f(1,0)=a,f(0,1)=b,
则f(x,y)=f(x,0)+f(0,y)=ax+by;
f(1,1)=1得a+b=1;
 得f(1,0)=f(0,
得f(1,0)=f(0, ),即a=
),即a=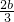 ,故a=
,故a= ,b=
,b= .
.所以f(x,y)=
 .
.故答案为:

点评:本题考查的知识点是抽象函数及其应用,其中根据已知条件设f(1,0)=a,f(0,1)=b,并构造关于a,b的方程组,是解答本题的关键.

练习册系列答案
相关题目