题目内容
如图所示,已知圆 的直径
的直径 长度为4,点
长度为4,点 为线段
为线段 上一点,且
上一点,且 ,点
,点 为圆
为圆 上一点,且
上一点,且 .点
.点 在圆
在圆 所在平面上的正投影为
所在平面上的正投影为
点 ,
, .
.

(1)求证: 平面
平面 ;
;
(2)求点 到平面
到平面 的距离.
的距离.
【答案】
(1)连接 ,由
,由 知,点
知,点 为
为 的中点,∵
的中点,∵ 为圆
为圆 的直径,∴
的直径,∴ 由
由 知,
知, ∴
∴ 为等边三角形,从而
为等边三角形,从而
 平面
平面 ,又
,又 平面
平面 由
由 得,
得, 平面
平面 (2)
(2)
【解析】
试题分析:(1)连接 ,由
,由 知,点
知,点 为
为 的中点,
的中点,
又∵ 为圆
为圆 的直径,∴
的直径,∴ ,
,
由 知,
知, ,
,
∴ 为等边三角形,从而
为等边三角形,从而 . 3分
. 3分
∵点 在圆
在圆 所在平面上的正投影为点
所在平面上的正投影为点 ,
,
∴ 平面
平面 ,又
,又 平面
平面 ,
,
∴ , 5分
, 5分
由 得,
得, 平面
平面 . 6分
. 6分
(2)由(1)可知 ,
, , 7分
, 7分
∴ . 10分
. 10分
又 ,
, ,
, ,
,
∴ 为等腰三角形,则
为等腰三角形,则 . 12分
. 12分
设点 到平面
到平面 的距离为
的距离为 ,由
,由 得,
得, ,解得
,解得 . 14分
. 14分
考点:线面垂直的判定及点面距
点评:证明直线垂直于平面,常用的方法是直线垂直于平面内两条相交直线,求点到平面的距离一般有两条思路:做出垂线段求其长度或利用等体积法转化为求三棱锥的高

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
 如图所示,一隧道内设双行线公路,其截面由一段圆弧和一个长方形构成.已知隧道总宽度AD为
如图所示,一隧道内设双行线公路,其截面由一段圆弧和一个长方形构成.已知隧道总宽度AD为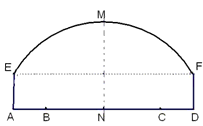 如图所示,一隧道内设双行线公路,其截面由一段圆弧和一个长方形构成.已知隧道总宽度AD为
如图所示,一隧道内设双行线公路,其截面由一段圆弧和一个长方形构成.已知隧道总宽度AD为 m,行车道总宽度BC为
m,行车道总宽度BC为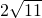 m,侧墙EA、FD高为2m,弧顶高MN为5m.
m,侧墙EA、FD高为2m,弧顶高MN为5m.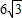 m,行车道总宽度BC为
m,行车道总宽度BC为 m,侧墙EA、FD高为2m,弧顶高MN为5m.
m,侧墙EA、FD高为2m,弧顶高MN为5m.