题目内容
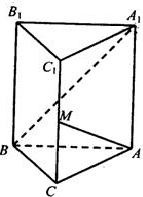
 三棱柱ABC-A1B1C1中,侧棱与底面垂直,∠ABC=90°,AB=BC=BB1=2,M,N分别是AB,A1C的中点.
三棱柱ABC-A1B1C1中,侧棱与底面垂直,∠ABC=90°,AB=BC=BB1=2,M,N分别是AB,A1C的中点.(1)求证:MN∥平面BCC1B1.
(2)求证:MN⊥平面A1B1C.
(3)求三棱锥M-A1B1C的体积.
分析:(Ⅰ)连接BC1,AC1,通过M,N是AB,A1C的中点,利用MN∥BC1.证明MN∥平面BCC1B1.
(Ⅱ)说明四边形BCC1B1是正方形,连接A1M,CM,通过△AMA1≌△AMC.说明MN⊥A1C然后证明MN⊥平面A1B1C.
(Ⅲ)由(Ⅱ)知MN是三棱锥M-A1B1C的高.在直角△MNC中.求出S△A1B1C=2
.即可解得VM-A1B1C=
MN•S△A1B1C=
.
(Ⅱ)说明四边形BCC1B1是正方形,连接A1M,CM,通过△AMA1≌△AMC.说明MN⊥A1C然后证明MN⊥平面A1B1C.
(Ⅲ)由(Ⅱ)知MN是三棱锥M-A1B1C的高.在直角△MNC中.求出S△A1B1C=2
| 2 |
| 1 |
| 3 |
| 4 |
| 3 |
解答: (Ⅰ)证明:连接BC1,AC1,∵在△ABC1中,M,N是AB,A1C的中点∴MN∥BC1.
(Ⅰ)证明:连接BC1,AC1,∵在△ABC1中,M,N是AB,A1C的中点∴MN∥BC1.
又∵MN不属于平面BCC1B1,∴MN∥平面BCC1B1.
(Ⅱ)解:∵三棱柱ABC-A1B1C1中,侧棱与底面垂直,
∴四边形BCC1B1是正方形.
∴BC1⊥B1C.∴MN⊥B1C.
连接A1M,CM,△AMA1≌△BMC.
∴A1M=CM,又N是A1C的中点,∴MN⊥A1C.
∵B1C与A1C相交于点C,
∴MN⊥平面A1B1C.
(Ⅲ)解:由(Ⅱ)知MN是三棱锥M-A1B1C的高.
在直角△MNC中,MC=
,A1C=2
,∴MN=
.
又S△A1B1C=2
.VM-A1B1C=
MN•S△A1B1C=
.
 (Ⅰ)证明:连接BC1,AC1,∵在△ABC1中,M,N是AB,A1C的中点∴MN∥BC1.
(Ⅰ)证明:连接BC1,AC1,∵在△ABC1中,M,N是AB,A1C的中点∴MN∥BC1.又∵MN不属于平面BCC1B1,∴MN∥平面BCC1B1.
(Ⅱ)解:∵三棱柱ABC-A1B1C1中,侧棱与底面垂直,
∴四边形BCC1B1是正方形.
∴BC1⊥B1C.∴MN⊥B1C.
连接A1M,CM,△AMA1≌△BMC.
∴A1M=CM,又N是A1C的中点,∴MN⊥A1C.
∵B1C与A1C相交于点C,
∴MN⊥平面A1B1C.
(Ⅲ)解:由(Ⅱ)知MN是三棱锥M-A1B1C的高.
在直角△MNC中,MC=
| 5 |
| 3 |
| 2 |
又S△A1B1C=2
| 2 |
| 1 |
| 3 |
| 4 |
| 3 |
点评:本题是中档题,考查空间线面关系、几何体的体积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力.

练习册系列答案
相关题目
 在三棱柱ABC-A1B1C1中,侧面AA1B1B是边长为2的正方形,点C在平面AA1B1B上的射影H恰好为A1B的中点,且CH=
在三棱柱ABC-A1B1C1中,侧面AA1B1B是边长为2的正方形,点C在平面AA1B1B上的射影H恰好为A1B的中点,且CH=
 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,∠BAC=30°,BC=1,
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,∠BAC=30°,BC=1, 如图:在直三棱柱ABC-A1B1C1中,已知AB=A1A,AC=BC,点D、E分别为C1C、AB的中点,O为A1B与AB1的交点.
如图:在直三棱柱ABC-A1B1C1中,已知AB=A1A,AC=BC,点D、E分别为C1C、AB的中点,O为A1B与AB1的交点.