题目内容
选修4—1:(本小题满分10分)几何证明选讲
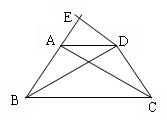
如图,在△ABC中,∠C为钝角,点E,
H分别是边AB上的点,点K和M分别
是边AC和BC上的点,且AH=AC,EB
=BC,AE=AK,BH=BM.
(Ⅰ)求证:E、H、M、K四点共圆;
(Ⅱ)若KE=EH,CE=3,求线段KM的
长.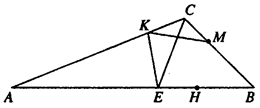
证明:⑴连接 ,
, ,
, 四边形
四边形 为等腰梯形,
为等腰梯形,
注意到等腰梯形的对角互补,
故 四点共圆,----------- 3分
四点共圆,----------- 3分
同理 四点共圆,
四点共圆,
即 均在点
均在点 所确定的圆上,证毕.--------------- 5分
所确定的圆上,证毕.--------------- 5分
⑵连结 ,
,
由⑴得 五点共圆,----------- 7分
五点共圆,----------- 7分
 为等腰梯形,
为等腰梯形, ,
,
故 ,
,
由 可得
可得 ,
,
故 ,
,
即 为所求. -------------------10分
为所求. -------------------10分
解析

练习册系列答案
相关题目
直线的参数方程为 (t为参数),则直线的倾斜角为( )
(t为参数),则直线的倾斜角为( )
A. | B. | C. | D. |
将参数方程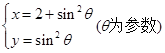 化为普通方程为( )
化为普通方程为( )
A.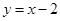 | B.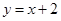 |
C.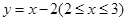 | D.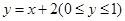 |
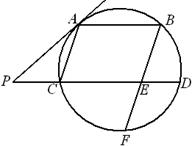

 是⊙
是⊙ 的直径,
的直径, 、
、 是⊙
是⊙ 是
是 的角平分线,过点
的角平分线,过点 ,交
,交 的延长线于
的延长线于 点,
点, ,垂足为点
,垂足为点 ,
,
 是⊙
是⊙
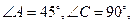
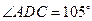 ,
,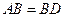 ,现将四边形ABCD沿BD折起,使平面ABD
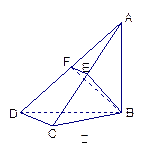
,现将四边形ABCD沿BD折起,使平面ABD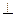 平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.
平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.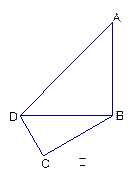
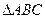 ≌
≌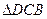 ;
; DC=AE
DC=AE