题目内容
已知以向量v=(1,
)为方向向量的直线l过点(0,
),抛物线C:y2=2px(p＞0)的顶点关于直线l的对称点在该抛物线的准线上.(1)求抛物线C的方程;
(2)设A、B是抛物线C上两个动点,过A作平行于x轴的直线m,直线OB与直线m交于点N,若
+p2=0(O为原点,A、B异于原点),试求点N的轨迹方程.
解：(1)由题意可得直线l:y=x+,①过原点垂直于l的直线方程为y=-2x.②
解①②,得x=.
∵抛物线的顶点关于直线l的对称点在该抛物线的准线上,∴-
=
×2,p=2.
∴抛物线C的方程为y2=4x.
(2)设A(x1,y1),B(x2,y2),N(x,y),由
+p2=0,得x1x2+y1y2+4=0,
又由y12=4x1,y22=4x2,解得y1y2=-8.③
直线ON:y=
x,即y=
x.④
由③④及y=y1,得点N的轨迹方程为x=-2(y≠0).
练习册系列答案
相关题目
)为方向向量的直线l过点(0, 
)，抛物线C：
(p>0)的顶点关于直线l的对称点在该抛物线上．
(O为原点，A、B异于原点)，试求点N的轨迹方程．
)为方向向量的直线l过点(0, 
(p>0)的顶点关于直线l的对称点在该抛物的准线上．
(O为原点，A、B异于原点)，试求点N的轨迹方程．
)为方向向量的直线l过点(0, 
)，抛物线C： 
(p>0)的顶点关于直线l的对称点在该抛物的准线上．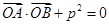
(O为原点，A、B异于原点)，试求点N的轨迹方程．