题目内容
圆: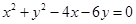 和圆:
和圆: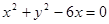 交于
交于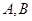 两点,则
两点,则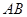 的垂直平分线的方程是( )
的垂直平分线的方程是( )
A.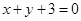 B
B 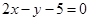 C
C 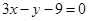 D
D 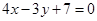
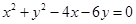 和圆:
和圆: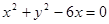 交于
交于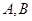 两点,则
两点,则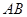 的垂直平分线的方程是( )
的垂直平分线的方程是( )A.
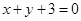 B
B 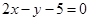 C
C 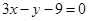 D
D 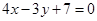
C
解:解:经过圆(x-2)2+(y-3)2=13和圆(x-3)2+y2=9交点的圆系方程为:(x-2)2+(y-3)2-13+λ[(x-3)2+y2-9]=0,
令λ=-1可得公共弦所在直线方程:3x+y-9=0,
就是弦AB的垂直平分线的方程.
故答案为:3x+y-9=0
令λ=-1可得公共弦所在直线方程:3x+y-9=0,
就是弦AB的垂直平分线的方程.
故答案为:3x+y-9=0

练习册系列答案
相关题目
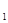 :
: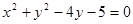 与圆
与圆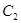 :
: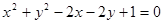 位置关系是( )
位置关系是( )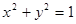 ,圆O1:
,圆O1: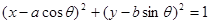 (
(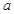 、
、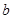 为常数,
为常数,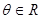 )对于以下命题,其中正确的有_______________.
)对于以下命题,其中正确的有_______________.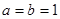 时,两圆上任意两点距离
时,两圆上任意两点距离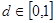
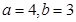 时,两圆上任意两点距离
时,两圆上任意两点距离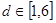
 ,存在定直线
,存在定直线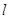 与两圆都相交
与两圆都相交 ,则经过圆
,则经过圆 的圆心,且焦点在
的圆心,且焦点在 轴上的抛物线标准方程是 .
轴上的抛物线标准方程是 .  和
和 关于直线
关于直线 对称,则
对称,则


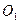 与⊙
与⊙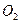 外
外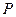 ,
,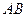 是两圆的外公切线,
是两圆的外公切线,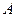 ,
,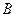 为切
为切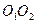 的延长线相交于点
的延长线相交于点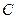 ,延长
,延长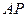
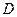 ,点
,点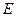 在
在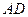 延长线上.
延长线上. 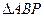 是直角三角形;
是直角三角形;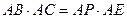 ,试判断
,试判断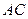 与
与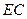 能否一定垂直?并说明理由.
能否一定垂直?并说明理由.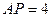 ,
,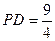 ,求
,求 的值.
的值.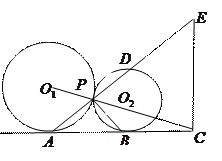
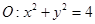 及点A(1,3),BC为
及点A(1,3),BC为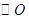 的任意一条直径,则
的任意一条直径,则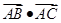 =( )
=( ) 关于原点对称的圆的方程为 ___ 。
关于原点对称的圆的方程为 ___ 。