题目内容
20.已知椭圆的焦距为4$\sqrt{3}$,椭圆上动点P与两个焦点距离乘积的最大值为13,则该椭圆的标准方程是$\frac{{x}^{2}}{13}+{y}^{2}$=1.分析 不妨设椭圆的焦点在x轴上,设椭圆标准方程为:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0).2c=4$\sqrt{3}$,由于|PF1||PF2|≤13,|PF1|+|PF2=2a≥2$\sqrt{|P{F}_{1}||P{F}_{2}|}$,可得a2,b2=a2-c2,即可得出.
解答 解:不妨设椭圆的焦点在x轴上,设椭圆标准方程为:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0).
2c=4$\sqrt{3}$,解得c=2$\sqrt{3}$.
|PF1||PF2|≤13,
|PF1|+|PF2=2a≥2$\sqrt{|P{F}_{1}||P{F}_{2}|}$,可得a2=13,b2=a2-c2=1.
∴该椭圆的标准方程是$\frac{{x}^{2}}{13}+{y}^{2}$=1.
故答案为:$\frac{{x}^{2}}{13}+{y}^{2}$=1.
点评 本题考查了椭圆的标准方程及其性质、基本不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
10.f(x)=$\frac{lnx}{x}$的极大值是( )
| A. | e | B. | $\frac{1}{e}$ | C. | -e | D. | -$\frac{1}{e}$ |
8.在△ABC中,若cosAcosB=-cos2$\frac{C}{2}$+1,则△ABC一定是( )
| A. | 等腰直角三角形 | B. | 直角三角形 | C. | 等腰三角形 | D. | 等边三角形 |
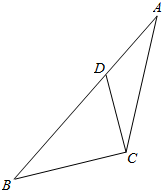 如图,在△ABC中,已知点D在AB边上,且$\overrightarrow{CB}$•$\overrightarrow{CD}$=0,sin∠ACB=$\frac{5\sqrt{7}}{14}$,AC=$\sqrt{7}$,AD=1.
如图,在△ABC中,已知点D在AB边上,且$\overrightarrow{CB}$•$\overrightarrow{CD}$=0,sin∠ACB=$\frac{5\sqrt{7}}{14}$,AC=$\sqrt{7}$,AD=1. 如图,已知PA⊥矩形ABCD所在的平面,M、N分别是AB、PC的中点,若AD=PA=a,$AB=\sqrt{2}a$.
如图,已知PA⊥矩形ABCD所在的平面,M、N分别是AB、PC的中点,若AD=PA=a,$AB=\sqrt{2}a$.