题目内容
设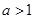 ,
,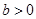 ,若
,若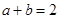 ,则
,则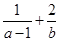 的最小值为
的最小值为
A.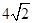 | B.6 | C.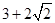 | D.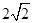 |
C
解析试题分析:∵a>1,b>0,a+b=2,∴a-1>0,a-1+b=1.
∴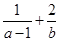 =[(a?1)+b](
=[(a?1)+b](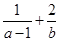 )=3+
)=3+

 .
.
当且仅当 ,即
,即 时取等号.
时取等号.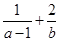 的最小值为
的最小值为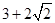 .故选:C.
.故选:C.
考点:基本不等式的性质

练习册系列答案
相关题目
对任意正数x,y不等式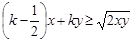 恒成立,则实数
恒成立,则实数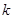 的最小值是 ( )
的最小值是 ( )
| A.1 | B.2 | C.3 | D.4 |
设a>0,b>0,若 是
是 和
和 的等比中项,则
的等比中项,则 的最小值为( )
的最小值为( )
| A.6 | B. | C.8 | D.9 |
(3分)(2011•重庆)已知a>0,b>0,a+b=2,则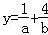 的最小值是( )
的最小值是( )
A.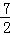 | B.4 | C.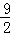 | D.5 |
下列结论正确的是 ( )
A.当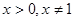 时, 时,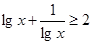 |
B.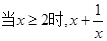 的最小值为 的最小值为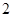 |
C.当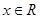 时, 时,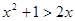 |
D.当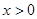 时, 时,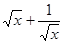 的最小值为 的最小值为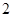 |
若实数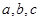 满足
满足 ,则
,则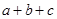 的最大值为( )
的最大值为( )
| A.9 | B. | C.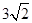 | D.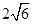 |
不等式x2+2x<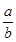 +
+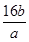 对任意a,b∈(0,+∞)恒成立,则实数x的取值范围是( )
对任意a,b∈(0,+∞)恒成立,则实数x的取值范围是( )
| A.(-2,0) | B.(-∞,-2)∪(0,+∞) |
| C.(-4,2) | D.(-∞,-4)∪(2,+∞) |
 是抛物线
是抛物线 的焦点,点
的焦点,点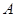 ,
, 在该抛物线上且位于
在该抛物线上且位于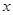 轴的两侧,
轴的两侧, (其中
(其中 为坐标原点),则
为坐标原点),则 与
与 面积之和的最小值是( )
面积之和的最小值是( )



 且
且
 时,求
时,求 的取值范围;
的取值范围; 时,求
时,求 的最小值.
的最小值.