[题目]某校200名学生的数学期中考试成绩频率分布直方图如图所示.其中成绩分组区间是(1)求图中的值,(2)根据频率分布直方图.估计这200名学生的平均分,(3)若这200名学生的数学成绩中.某些分数段的人数与英语成绩相应分数段的人数之比如表所示.求英语成绩在的人数. 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】某校200名学生的数学期中考试成绩频率分布直方图如图所示，其中成绩分组区间是

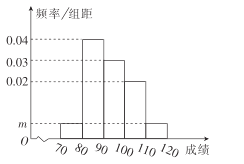
（1）求图中的值；

（2）根据频率分布直方图，估计这200名学生的平均分；

（3）若这200名学生的数学成绩中，某些分数段的人数与英语成绩相应分数段的人数之比如表所示，求英语成绩在的人数.

【答案】（1）（2）93 （3）140

【解析】

（1）由频率分布直方图求出的值；

（2）根据频率分布直方图估计这200名学生的平均分；

（3）这200名学生的数学成绩在的分别有60人，40人，10人，按照表中给出的比例，则英语成绩在的分别有50人，80人，10人，由此可求出结果.

解：（1）由频率分布直方图，得

解得

（2）由频率分布直方图，估计这200名学生的平均分为：

（3）这200名学生的数学成绩在的分别有60人，40人，10人，按照表中给出的比例，则英语成绩在的分别有50人，80人，10人，所以英语成绩在的有140人.

练习册系列答案

（1）求a，b的值

（2）求f（x）在[﹣4，4]内的最值.

【题目】2018年国际象棋奥林匹克团体赛中国男队、女队同时夺冠.国际象棋中骑士的移动规则是沿着3×2格或2×3格的对角移动.在历史上，欧拉、泰勒、哈密尔顿等数学家研究了“骑士巡游”问题：在格的黑白相间的国际象棋棋盘上移动骑士，是否可以让骑士从某方格内出发不重复地走遍棋盘上的每一格？

图（一）给出了骑士的一种走法，它从图上标1的方格内出发，依次经过标2,3,4,5,6,,到达标64的方格内，不重复地走遍棋盘上的每一格，又可从标64的方格内直接走回到标1的方格内.如果骑士的出发点在左下角标50的方格内，按照上述走法，_____（填“能”或“不能”）走回到标50的方格内.

若骑士限制在图（二）中的3×4=12格内按规则移动，存在唯一一种给方格标数字的方式，使得骑士从左上角标1的方格内出发，依次不重复经过2,3,4,5,6,,到达右下角标12的方格内，分析图（二）中A处所标的数应为____.

【题目】函数f(x)＝2x和g(x)＝2x的图象如图所示，设两函数的图象交于点A(x1，y1)，B(x2，y2)，且x1＜x2.

（1）请指出图中曲线C1，C2分别对应的函数；

（2）结合函数图象，判断与，f(2 019)与g(2 019)的大小．

【题目】已知三棱锥的所有顶点都在球的球面上，平面，，，若球的表面积为，则三棱锥的侧面积的最大值为（）

A. B. C. D.

【题目】在△ABC中，内角A，B，C所对的边分别为a，b，c，cosB＝．

（Ⅰ）若c＝2a，求的值；

（Ⅱ）若C－B＝，求sinA的值．

【题目】某超市在节日期间进行有奖促销，凡在该超市购物满元的顾客，将获得一次摸奖机会，规则如下：一个袋子装有只形状和大小均相同的玻璃球，其中两只是红色，三只是绿色，顾客从袋子中一次摸出两只球，若两只球都是红色，则奖励元；共两只球都是绿色，则奖励元；若两只球颜色不同，则不奖励．

（1）求一名顾客在一次摸奖活动中获得元的概率；

（2）记为两名顾客参与该摸奖活动获得的奖励总数额，求随机变量的分布列和数学期望．

【题目】某单位用2160万元购得一块空地，计划在该空地上建造一栋至少10层，每层2000平方米的楼房．经测算，如果将楼房建为x（x≥10）层，则每平方米的平均建筑费用为560＋48x（单位：元）．

（1）写出楼房平均综合费用y关于建造层数x的函数关系式；

（2）该楼房应建造多少层时，可使楼房每平方米的平均综合费用最少？最少值是多少？

（注：平均综合费用＝平均建筑费用＋平均购地费用，平均购地费用＝购地总费用/建筑总面积）

【题目】为提高玉米产量，某种植基地对单位面积播种数与每棵作物的产量之间的关系进行了研究，收集了块试验田的数据，得到下表：

试验田编号
（棵/）
（斤/棵）

技术人员选择模型作为与的回归方程类型，令，相关统计量的值如下表：

由表中数据得到回归方程后进行残差分析，残差图如图所示：

（1）根据残差图发现一个可疑数据，请写出可疑数据的编号（给出判断即可，不必说明理由）；

（2）剔除可疑数据后，由最小二乘法得到关于的线性回归方程中的，求关于的回归方程；

（3）利用（2）得出的结果，计算当单位面积播种数为何值时，单位面积的总产量的预报值最大？（计算结果精确到）

附：对于一组数据，，，其回归直线的斜率和截距的最小二乘法估计分别为，，

试题分类