题目内容
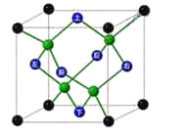
【题目】金刚石是碳原子的一种结构晶体，属于面心立方晶胞（晶胞是构成晶体的最基本的几何单元），即碳原子处在立方体的
个顶点，
个面的中心，此外在立方体的对角线的
处也有
个碳原子，如图所示（绿色球），碳原子都以共价键结合，原子排列的基本规律是每一个碳原子的周围都有个按照正四面体分布的碳原子．设金刚石晶胞的棱长为
，则正四面体
的棱长为__________；正四面体的外接球的体积是__________．
【答案】
【解析】
依题意可知，
为正四面体
的中心，
，设
利用勾股定理
即可解得
，从而可得正四面体的外接球的半径，进而可求出体积.
依题意可知，为正四面体的中心，如图：
连接
，延长交平面
于点
，则为△的中心，
所以设，
，
因为
，所以
，
由，得
，
得
，解得
，
所以正四面体的棱长为
.
依题意可知，正四面体的外接球的圆心为，半径为
，
所以正四面体的外接球的体积是
.
故答案为：；.
练习册系列答案
春雨教育同步作文系列答案
相关题目
