题目内容
数列{an}中,如果存在ak,使得“ak>ak-1且ak>ak+1”成立(其中k≥2,k∈N*),则称ak为{an}的一个峰值.(Ⅰ)若an=-|n-7|,则{an}的峰值为 ;
(Ⅱ)若
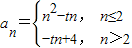 且{an}存在峰值,则实数t的取值范围是 .
且{an}存在峰值,则实数t的取值范围是 .
【答案】分析:(Ⅰ)根据峰值的定义,可得an=-|n-7|,求出数列函数的单调性求出最值,从而求解;
(Ⅱ)已知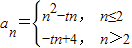 且{an}存在峰值,还是求出数列函数的单调性,再进行求解;
且{an}存在峰值,还是求出数列函数的单调性,再进行求解;
解答:解:(Ⅰ)∵数列{an}中,如果存在ak,使得“ak>ak-1且ak>ak+1”成立(其中k≥2,k∈N*),
则称ak为{an}的一个峰值,即是数列中的最大值,
an=-|n-7|≤0,最大值就是0,可得n=7时,an=0,当n>7或n<7都有an<0,
∴{an}的峰值为0;
(Ⅱ)当n≤2时,有f(n)=an=n2-tn=(n- )2-
)2-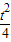 ,开口向上,对称轴为
,开口向上,对称轴为 ,
,
在n≤ 时,f(n)为增函数,
时,f(n)为增函数,
当n>2,g(n)=an=-tn+4,是减函数,但是一个一个的孤立点,
因为{an}存在峰值,说明n=2处取得,说明-t必须小于0,可得,
-t<0,可得t>0,说明n=2处取得最大值,
n=2,f(2)=4-2t,
根据峰值的定义可得,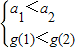 ,
,
可得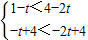 ,
,
解得0<t<3
故答案为:0,0<t<3;
点评:此题是一道新定义题,主要考查数列的函数的特性,是一道中档题,考查的知识点比较全面;
(Ⅱ)已知
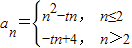 且{an}存在峰值,还是求出数列函数的单调性,再进行求解;
且{an}存在峰值,还是求出数列函数的单调性,再进行求解;解答:解:(Ⅰ)∵数列{an}中,如果存在ak,使得“ak>ak-1且ak>ak+1”成立(其中k≥2,k∈N*),
则称ak为{an}的一个峰值,即是数列中的最大值,
an=-|n-7|≤0,最大值就是0,可得n=7时,an=0,当n>7或n<7都有an<0,
∴{an}的峰值为0;
(Ⅱ)当n≤2时,有f(n)=an=n2-tn=(n-
 )2-
)2-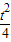 ,开口向上,对称轴为
,开口向上,对称轴为 ,
,在n≤
 时,f(n)为增函数,
时,f(n)为增函数,当n>2,g(n)=an=-tn+4,是减函数,但是一个一个的孤立点,
因为{an}存在峰值,说明n=2处取得,说明-t必须小于0,可得,
-t<0,可得t>0,说明n=2处取得最大值,
n=2,f(2)=4-2t,
根据峰值的定义可得,
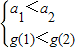 ,
,可得
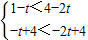 ,
,解得0<t<3
故答案为:0,0<t<3;
点评:此题是一道新定义题,主要考查数列的函数的特性,是一道中档题,考查的知识点比较全面;

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
在数列{an}中,如果an+1=
an+1,(n∈N*),且a1=1,则a4等于( )
| 1 |
| 2 |
| A、4 | ||
B、
| ||
C、
| ||
D、
|