题目内容
若一个变换所对应的矩阵是
,则抛物线y2=-4x在这个变换下所得到的曲线的方程是( )
|
分析:确定变换前后点的坐标之间的关系,利用变换前的点在抛物线上,即可得到变换后曲线的方程.
解答:解:设抛物线y2=-4x上的点(a,b)在变换下变为(x,y),则
=
∴
,∴
∵(a,b)满足抛物线y2=-4x
∴b2=-4a
∴
=4x
∴y2=16x
故选D.
|
|
|
∴
|
|
∵(a,b)满足抛物线y2=-4x
∴b2=-4a
∴
| y2 |
| 4 |
∴y2=16x
故选D.
点评:本题考查矩阵变换,考查求曲线方程,解题的关键是确定变换前后点的坐标之间的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


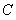
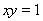
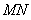
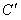
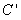
 ,则抛物线y2=-4x在这个变换下所得到的曲线的方程是( )
,则抛物线y2=-4x在这个变换下所得到的曲线的方程是( ) ,则抛物线y2=-4x在这个变换下所得到的曲线的方程是( )
,则抛物线y2=-4x在这个变换下所得到的曲线的方程是( )