题目内容
若M,N分别是曲线ρ=2cosθ和ρsin(θ-
)=
上的动点,则M,N两点间的距离的最小值是
-1
-1.
| π |
| 4 |
| ||
| 2 |
| 2 |
| 2 |
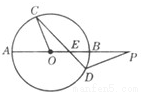
分析:可以先将极坐标方程化为直角坐标方程,M、N是直线与圆上的两个动点,最小距离为圆心到直线的距离减去半径即可.
解答:解:曲线ρ=2cosθ和ρsin(θ-
)=
,
可化为直角坐标方程为:x-y+1=0与(x-1)2+y2=1
∴M、N在直线与圆心(1,0)半径为1的圆上
圆心(1,0)到直线的距离d=
=
∴M,N两点间的距离的最小值dmin=
-1.
故答案为:
-1.
| π |
| 4 |
| ||
| 2 |
可化为直角坐标方程为:x-y+1=0与(x-1)2+y2=1
∴M、N在直线与圆心(1,0)半径为1的圆上
圆心(1,0)到直线的距离d=
| |2| | ||
|
| 2 |
∴M,N两点间的距离的最小值dmin=
| 2 |
故答案为:
| 2 |
点评:本题考查极坐标与直角坐标之间的转化,点到直线的距离,考查计算能力.

练习册系列答案
相关题目
 选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)
选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分) 选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)
选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分) 上的动点,则M,N两点间的距离的最小值是 ;
上的动点,则M,N两点间的距离的最小值是 ;
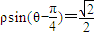 上的动点,则M,N两点间的距离的最小值是 .
上的动点,则M,N两点间的距离的最小值是 .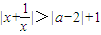 对于一切非零实数x均成立,则实数a的取值范围为 .
对于一切非零实数x均成立,则实数a的取值范围为 .