题目内容
已知数列{an}为各项均为正的等比数列,其公比为q.
(1)当q=
时,在数列{an}中:
①最多有几项在1~100之间?
②最多有几项是1~100之间的整数?
(2)当q>1时,在数列{an}中,最多有几项是100~1000之间的整数?(参考数据:lg3=0.477,lg2=0.301).
(1)当q=
| 3 |
| 2 |
①最多有几项在1~100之间?
②最多有几项是1~100之间的整数?
(2)当q>1时,在数列{an}中,最多有几项是100~1000之间的整数?(参考数据:lg3=0.477,lg2=0.301).
(1)①不妨设a1≥1,设数列an有n项在1和100之间,则a1•(
)n-1≤100.所以,(
)n-1≤100.
两边同取对数,得(n-1)(lg3-lg2)≤2.解之,得n≤12.37.
故n的最大值为12,即数列an中,最多有12项在1和100之间.(5分)
②不妨设1≤a1<a1•
<a1•(
)2<<a1•(
)n-1≤100,其中a1,a1•
,a1•(
)2,,a1•(
)n-1均为整数,所以a1为2n-1的倍数.所以3n-1≤100,所以n≤5.(8分)
又因为16,24,36,54,81是满足题设要求的5项.
所以,当q=
时,最多有5项是1和100之间的整数.(10分)
(2)设等比数列aqn-1满足100≤a<aq<<aqn-1≤1000,
其中a,aq,,aqn-1均为整数,n∈N*,q>1,显然,q必为有理数.(11分)
设q=
,t>s≥1,t与s互质,
因为aqn-1=a(
)n-1为整数,所以a是sn-1的倍数.(12分)
令t=s+1,于是数列满足100≤a<a•
<<a•(
)n-1≤100.
如果s≥3,则1000≥a•(
)n-1≥(q+1)n-1≥4n-1,所以n≤5.
如果s=1,则1000≥a•2n-1≥100•2n-1,所以,n≤4.
如果s=2,则1000≥a•(
)n-1≥100•(
)n-1,所以n≤6.(13分)
另一方面,数列128,192,288,432,648,972满足题设条件的6个数,
所以,当q>1时,最多有6项是100到1000之间的整数.(16分)
| 3 |
| 2 |
| 3 |
| 2 |
两边同取对数,得(n-1)(lg3-lg2)≤2.解之,得n≤12.37.
故n的最大值为12,即数列an中,最多有12项在1和100之间.(5分)
②不妨设1≤a1<a1•
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
又因为16,24,36,54,81是满足题设要求的5项.
所以,当q=
| 3 |
| 2 |
(2)设等比数列aqn-1满足100≤a<aq<<aqn-1≤1000,
其中a,aq,,aqn-1均为整数,n∈N*,q>1,显然,q必为有理数.(11分)
设q=
| t |
| s |
因为aqn-1=a(
| t |
| s |
令t=s+1,于是数列满足100≤a<a•
| s+1 |
| s |
| s+1 |
| s |
如果s≥3,则1000≥a•(
| s+1 |
| s |
如果s=1,则1000≥a•2n-1≥100•2n-1,所以,n≤4.
如果s=2,则1000≥a•(
| 3 |
| 2 |
| 3 |
| 2 |
另一方面,数列128,192,288,432,648,972满足题设条件的6个数,
所以,当q>1时,最多有6项是100到1000之间的整数.(16分)

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
 已知数列{an},a1=1,an+1=an+2n,计算数列{an}前10项的和;现已给出了该问题算法的程序框图(如图所示),
已知数列{an},a1=1,an+1=an+2n,计算数列{an}前10项的和;现已给出了该问题算法的程序框图(如图所示), ,则下列各数是否为数列中的项?如果是,是第几项?如果不是,为什么?(1)
,则下列各数是否为数列中的项?如果是,是第几项?如果不是,为什么?(1) (2)
(2)
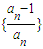 的前n项积,是否存在实数a,使得不等式
的前n项积,是否存在实数a,使得不等式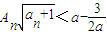 对一切n∈N*都成立?若存在,求出a的取值范围;若不存在,请说明理由.
对一切n∈N*都成立?若存在,求出a的取值范围;若不存在,请说明理由.