题目内容
(本小题满分12分)
设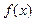 是定义域为
是定义域为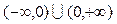 的奇函数,且它在区间
的奇函数,且它在区间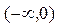 上单调增.
上单调增.
(1)用定义证明: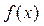 在
在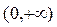 上的单调性;
上的单调性;
(2)若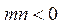 且
且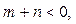 试判断
试判断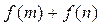 的符号;
的符号;
(3)若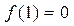 解关于
解关于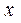 的不等式
的不等式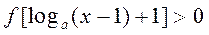 .
.
设
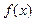 是定义域为
是定义域为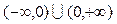 的奇函数,且它在区间
的奇函数,且它在区间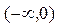 上单调增.
上单调增.(1)用定义证明:
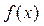 在
在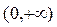 上的单调性;
上的单调性;(2)若
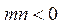 且
且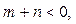 试判断
试判断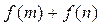 的符号;
的符号;(3)若
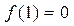 解关于
解关于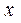 的不等式
的不等式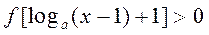 .
.(1)函数在
 上递增函数
上递增函数(2)

(3)
当
 时,
时, 或
或
当
 时,
时, 或
或
(本小题满分14分)
解:(1)设 ,且
,且
则 ,且
,且 ,由已知函数在
,由已知函数在 上单调递增,得:
上单调递增,得:
 ,又函数是奇函数,有
,又函数是奇函数,有
即 ,得到:
,得到: ,所以函数在
,所以函数在 上递增函数。
上递增函数。
(2)不妨设 ,则由已知
,则由已知
 ,已知函数在
,已知函数在 上递增,故有:
上递增,故有: ,得
,得
(3)由 及函数在
及函数在 和
和 上递增可知:
上递增可知:
 或
或
即 或
或
当 时,
时, 或
或
当 时,
时, 或
或
解:(1)设
 ,且
,且
则
 ,且
,且 ,由已知函数在
,由已知函数在 上单调递增,得:
上单调递增,得: ,又函数是奇函数,有
,又函数是奇函数,有
即
 ,得到:
,得到: ,所以函数在
,所以函数在 上递增函数。
上递增函数。(2)不妨设
 ,则由已知
,则由已知
 ,已知函数在
,已知函数在 上递增,故有:
上递增,故有: ,得
,得
(3)由
 及函数在
及函数在 和
和 上递增可知:
上递增可知: 或
或
即
 或
或
当
 时,
时, 或
或
当
 时,
时, 或
或

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
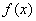 对任意
对任意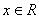 ,都有
,都有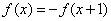 ,当
,当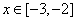 时,
时,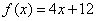 ,则
,则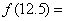 ( )
( )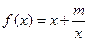 ,且此函数图像过点(1,5).
,且此函数图像过点(1,5).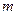 的值;
的值;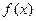 奇偶性;
奇偶性;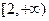 上的单调性,并用定义证明你的结论.
上的单调性,并用定义证明你的结论. 的不等式
的不等式 ,
,  时,解上述不等式;
时,解上述不等式; 时,若上述不等式恒成立,求实数
时,若上述不等式恒成立,求实数 的取值范围。
的取值范围。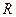 上的不恒为零的函数
上的不恒为零的函数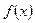 ,且对于任意实数
,且对于任意实数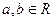 ,满足
,满足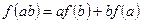 ,
,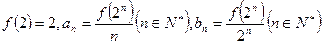 ,考察下列结论:①
,考察下列结论:①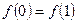 ;②
;②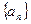 为等比数列;④
为等比数列;④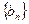 为等差数列;其中正确命题的序号为____________.
为等差数列;其中正确命题的序号为____________. 是定义在R上的偶函数,当
是定义在R上的偶函数,当 <0时,
<0时, 是单调递增的,则不等式
是单调递增的,则不等式 >
> 的解集是_______________
的解集是_______________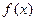 的定义域为D,若对于任意的
的定义域为D,若对于任意的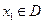 ,存在唯一的
,存在唯一的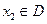 ,使
,使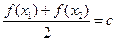 (c为常数)成立,则称函数
(c为常数)成立,则称函数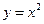 ②
②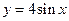 ③
③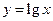 ④
④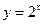 ,则满足其定义域上均值为2的所有函数的序号为 。
,则满足其定义域上均值为2的所有函数的序号为 。 ,则满足
,则满足 的
的 值是_______.
值是_______.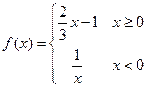 ,若
,若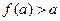 ,则实数a的取值范围是 ( )
,则实数a的取值范围是 ( )

