题目内容
已知A(0,3),B(-1,0),C(3,0),求D点的坐标,使四边形ABCD为直角梯形(A、B、C、D按逆时针方向排列).
答案:略
解析:
解析:
|
思维分析:由直角梯形的知识,若 ABCD为直角梯形,则必有一边垂直于与它相邻的两边,且这一边与它相对的边不平行,因此可设出点D(x,y),将各边的斜率表示出来之后,建立斜率之间的关系即可.解:设所求点 D的坐标为(x,y),如图,由于 =3, =3, =0,∴即AB与BC不垂直,故AB、BC都不可作为直角梯形的直角边. =0,∴即AB与BC不垂直,故AB、BC都不可作为直角梯形的直角边.
( 1)若CD是直角梯形的直角边,则BC⊥CD,AD⊥CD,∵ =0,∴CD的斜率不存在。从而有x=3.又 =0,∴CD的斜率不存在。从而有x=3.又 = = ,∴ ,∴ ,即y=3此时AB与CD不平行.故所求点D的坐标为(3,3). ,即y=3此时AB与CD不平行.故所求点D的坐标为(3,3).
(2) 若AD是直角梯形的直角边,则AD⊥AB,且AD⊥CD,∵ , , 由于AD⊥AB,又AB∥CD,∴ 由于AD⊥AB,又AB∥CD,∴ ·3=-1.解上述两式可得 ·3=-1.解上述两式可得 :此时AD与BC不平行.综上可知,使ABCD为直角梯形的点D的坐标可以为(3,3)和( :此时AD与BC不平行.综上可知,使ABCD为直角梯形的点D的坐标可以为(3,3)和( , , ). ).
点拨: (1)把哪条边作为直角梯形的直角腰是分类的标准,解决此题时要注意不要丢根(2)在遇到两条直线的平行或垂直的问题时,一定要注意直线的斜率不存在时的情形,如本例中的CD作为直角腰时,其斜率便不存在 |

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目

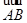 、
、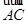 、
、 ;
;