题目内容
已知A(0,3),B(-1,0),C(3,0),求D点的坐标,使四边形ABCD为直角梯形(A、B、C、D按逆时针方向排列).
【探究】 解:设所求点D的坐标为(x、y),由于kAB=3,kBC=0,
∴kAB·kBC=0≠-1,
即AB与BC不垂直,
故AB、BC都不可作为直角梯形的直角边.
(1)若CD是直角梯形的直角边,
则BC⊥CD,AD⊥CD.
∵kBC=0,∴CD的斜率不存在,从而有x=3.
又kAD=kBC,∴![]() ,即y=3.
,即y=3.
此时AB与CD不平行.
故所求点D的坐标为(3,3).
(2)若AD是直角梯形的直角边,则AD⊥AB,AD⊥CD.
∵kAD=![]() ,kCD=
,kCD=![]() ,
,
又由于AD⊥AB,∴![]() .
.
又AB∥CD,∴![]() .解上述两式可得
.解上述两式可得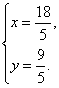
此时AD与BC不平行.
综上可知,使ABCD为直角梯形的点D的坐标可以为(3,3)和![]() .
.
【规律总结】 (1)把哪条边作为直角梯形的直角腰是分类的标准,解决此题时要注意不要丢下基础的东西.
(2)在遇到两条直线的平行或垂直的问题时,一是要注意直线的斜率不存在时的情形,如本例中的CD作为直角腰时,其斜率便不存在.

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
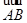 、
、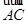 、
、 ;
;