Question

从圆C:x²+y²-4x-6y+12=0外一点P(a,b)向圆作切线PT,T为切点,且|PT|=|PO|(O为原点),求|PT|的最小值以及此刻点P的坐标.

Answer 1

解：由已知,圆C的方程为(x-2)²+(y-3)²=1,圆心C的坐标是(2,3),半径长r=1.

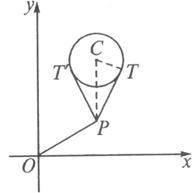
如下图,连结PC、CT.由平面几何,知

|PT|²=|PC|²-|CT|²=(a-2)²+(b-3)²-1.

由已知,得|PT|=|PO|.

所以|PT|²=|PO|²,

即(a-2)²+(b-3)²-1=a²+b².

化简,得2a+3b-6=0,                           ①

|PT|²=|PO|²=a²+b².                            ②

①②消去b,得|PT|²=(13a²-24a+36).

当a=时,

|PT|_min=.

|PT|的最小值为,此刻点P的坐标是().