题目内容
【题目】如图，F1、F2是双曲线 
=1（a＞0）的左、右焦点，过F1的直线l与双曲线交于点A、B，若△ABF2为等边三角形，则△BF1F2的面积为（ ） 
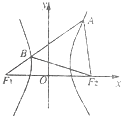
A.8
B.8 
C.8 
D.16
【答案】C
【解析】解：根据双曲线的定义，可得|BF1|﹣|BF2|=2a， ∵△ABF2是等边三角形，即|BF2|=|AB|
∴|BF1|﹣|BF2|=2a，即|BF1|﹣|AB|=|AF1|=2a
又∵|AF2|﹣|AF1|=2a，
∴|AF2|=|AF1|+2a=4a，
∵△AF1F2中，|AF1|=2a，|AF2|=4a，∠F1AF2=120°
∴|F1F2|2=|AF1|2+|AF2|2﹣2|AF1||AF2|cos120°
即4c2=4a2+16a2﹣2×2a×4a×（﹣ 
）=28a2 ， 解之得c= 
a，
∴a2+24=7a2 ， ∴a=2，
∴△BF1F2的面积为 
﹣ 
= 
﹣ 
=8 
．
故选：C．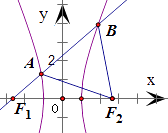
练习册系列答案
相关题目
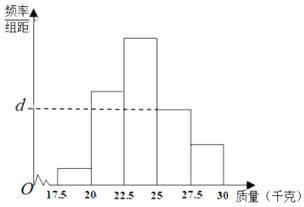
【题目】为了检测某种产品的质量（单位：千克），抽取了一个容量为N的样本，整理得到的数据作出了频率分布表和频率分布直方图如图：
分组 | 频数 | 频率 |
[17.5，20） | 10 | 0.05 |
[20，225） | 50 | 0.25 |
[22.5，25） | a | b |
[25，27.5） | 40 | c |
[27.5，30] | 20 | 0.10 |
合计 | N | 1 |
（Ⅰ）求出表中N及a，b，c的值；
（Ⅱ）求频率分布直方图中d的值；
（Ⅲ）从该产品中随机抽取一件，试估计这件产品的质量少于25千克的概率．