Question

如图,在正方体ABCD—A₁B₁C₁D₁中,E为AB的中点.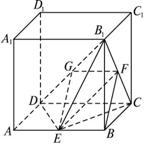

(1)求AD和B₁C所成的角;

(2)证明平面EB₁D⊥平面B₁CD;

(3)求二面角EB₁CD的大小(用反三角函数表示).

Answer 1

解法一:(1)解:正方体ABCD—A₁B₁C₁D₁中,AD∥BC,

∴AD与B₁C所成的角为∠B₁CB或其补角.                                    

∵∠B₁CB=45°,

∴AD和B₁C所成的角为45°.                                               

(2)证明:取B₁C的中点F,B₁D的中点G,

连结BF、EG、GF.

∵CD⊥平面BCC₁B₁,

∴DC⊥BF.

又BF⊥B₁C,DC∩B₁C=C,

∴BF⊥平面B₁CD.                                                        

∵CFCD,BECD,

∴BEGF.

∴四边形BFGE是平行四边形.

∴BF∥GE.

∴EG⊥平面B₁CD.                                                       

又EG平面EB₁D,

∴平面EB₁D⊥平面B₁CD.                                                 

(3)解:连结EF.

∵CD⊥B₁C,GF∥CD,

∴GF⊥B₁C.

又EG⊥平面B₁CD,EF⊥B₁C,

∴∠EFG为二面角EB₁CD的平面角.                                        

设正方体的棱长为a,则在△EFG中,

GF=a,EF=a,

∴cos∠EFG==.                                                 

∴二面角E-B₁C-D的大小为arccos.                                     

解法二:不妨设正方体的棱长为2个长度单位,且设=i, =j,=k.

以i、j、k为坐标向量建立如图所示的空间直角坐标系D—xyz.

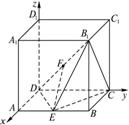
(1)解:∵D(0,0,0),A(2,0,0),C(0,2,0),B₁(2,2,2),

∴=(2,0,0), =(2,0,2),                                                

cos〈,〉===.

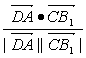∴AD与B₁C所成的角为45°.                                                

(2)证明:取B₁D的中点F,连结EF.∵F(1,1,1)、E(2,1,0),

∴=(-1,0,1), =(0,2,0), ·=0, ·=0.             

∴EF⊥CD,EF⊥CB₁.

∵CD与CB₁相交,

∴EF⊥平面B₁CD.                                                         

又EF平面EB₁D,∴平面EB₁D⊥平面B₁CD.                                   

(3)解:设平面B₁CD的法向量m=(1,a,b),

由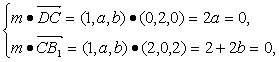

解得c=0,b=-1,∴m=(1,0,-1).                                                  

设平面EB₁C的法向量n=(-1,c,d).

由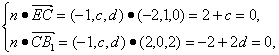

解得c=-2,d=1,∴n=(-1,-2,1).                                                

∴cos〈m,n〉===-.                                     

∴二面角EB₁CD的大小为arccos.