题目内容
已知集合A={x||x-1|>a,a>0 },集合B={x|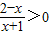 ,x∈Z},若A∩B=∅,试求实数a的取值范围.
,x∈Z},若A∩B=∅,试求实数a的取值范围.
【答案】分析:把集合A、B化简,由两集合的交集是空集得到两集合端点值的关系,从而求出a的范围.
解答:解:A={ x|x>1+a或x<1-a,a>0 },…(2分)
B={ x|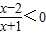 ,x∈Z }={ x|-1<x<2,x∈Z }={ 0,1 }.
,x∈Z }={ x|-1<x<2,x∈Z }={ 0,1 }.
…(4分)因为A∩B=∅,所以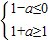 …(8分)
…(8分)
解得a≥1为所求. …(10分)
另法:
A={ x||x-1|>a,a>0 },B={ x|-1<x<2,x∈Z }={ 0,1 }.
因为A∩B=∅,所以0∉A,1∉A,于是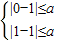 ,
,
得a≥1.
点评:本题考查了交集及其运算,考查了不等式的解法,是基础题.
解答:解:A={ x|x>1+a或x<1-a,a>0 },…(2分)
B={ x|
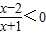 ,x∈Z }={ x|-1<x<2,x∈Z }={ 0,1 }.
,x∈Z }={ x|-1<x<2,x∈Z }={ 0,1 }.…(4分)因为A∩B=∅,所以
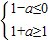 …(8分)
…(8分)解得a≥1为所求. …(10分)
另法:
A={ x||x-1|>a,a>0 },B={ x|-1<x<2,x∈Z }={ 0,1 }.
因为A∩B=∅,所以0∉A,1∉A,于是
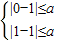 ,
,得a≥1.
点评:本题考查了交集及其运算,考查了不等式的解法,是基础题.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目