题目内容
设函数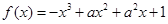 (
(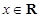 ),其中
),其中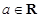 .
.
(Ⅰ)当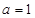 时,求曲线
时,求曲线 在点
在点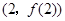 处的切线方程;
处的切线方程;
(Ⅱ)当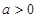 时,求函数
时,求函数 的极大值和极小值.
的极大值和极小值.
(Ⅰ)当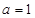 时,曲线
时,曲线 在点
在点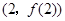 处的切线方程为
处的切线方程为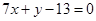 ;(Ⅱ)函数
;(Ⅱ)函数 在
在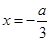 处取得极小值
处取得极小值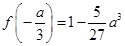 ,在
,在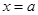 处取得极大值
处取得极大值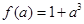 .
.
解析试题分析:(Ⅰ)把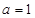 代入
代入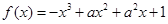 ,得
,得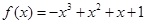 ,结合已知条件即可得切点的坐标为
,结合已知条件即可得切点的坐标为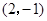 .再对
.再对 求导,即可求得
求导,即可求得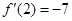 ,即可得所求切线的斜率,最后利用直线方程的点斜式,即可得所求切线的方程;(Ⅱ)首先对
,即可得所求切线的斜率,最后利用直线方程的点斜式,即可得所求切线的方程;(Ⅱ)首先对 求导,得
求导,得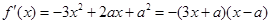 .令
.令 ,解得
,解得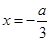 或
或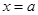 .
.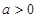 ,列出当
,列出当 变化时,
变化时, ,
,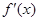 随
随 的变化情况表格,即可求得当
的变化情况表格,即可求得当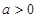 时,函数
时,函数 的极大值和极小值.
的极大值和极小值.
试题解析:(Ⅰ)当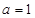 时,
时,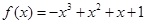 ,得
,得 , 1分
, 1分
且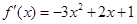 ,
,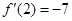 . 3分
. 3分
所以,曲线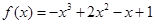 在点
在点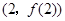 处的切线方程是
处的切线方程是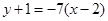 , 5分
, 5分
整理得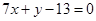 . 6分
. 6分
(Ⅱ)解: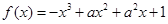 ,
, .
.
令 ,解得
,解得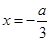 或
或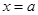 . 8分
. 8分
若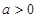 ,当
,当 变化时,
变化时,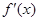 的正负如下表:
的正负如下表:
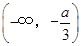
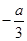
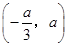

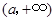
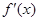
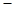
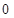
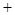
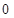
 练习册系列答案
练习册系列答案
智多星归类复习测试卷系列答案
智多星模拟加真题测试卷系列答案
毕业升学考卷大集结系列答案
毕业升学冲刺必备方案系列答案
状元坊广东中考备考用书系列答案
百年学典中考风向标系列答案
百校联盟中考冲刺名校模拟卷系列答案
夺A闯关一路领先中考模拟密卷系列答案
中考先锋滚动迁移复习法系列答案
琢玉计划寒假生活系列答案
相关题目
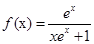 .
.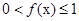 ;
;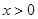 时,
时,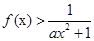 ,求
,求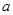 的取值范围.
的取值范围.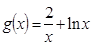 ,
,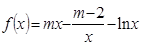 ,
,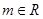 .
.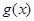 的极值点;
的极值点;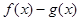 在
在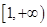 上为单调函数,求
上为单调函数,求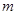 的取值范围;
的取值范围;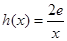 ,若在
,若在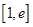 上至少存在一个
上至少存在一个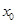 ,使得
,使得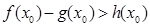 成立,求
成立,求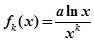 为
为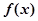 的
的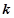 阶函数.
阶函数.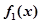 的单调区间;
的单调区间;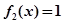 的解的个数;
的解的个数; .
. .
.
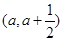 其中
其中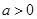 上存在极值,求实数
上存在极值,求实数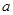 的取值范围;
的取值范围;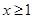 时,不等式
时,不等式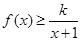 恒成立,求实数
恒成立,求实数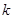 的取值范围.
的取值范围.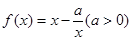 ,
,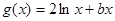 ,且直线
,且直线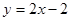 与曲线
与曲线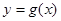 相切.
相切.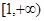 内的一切实数
内的一切实数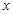 ,不等式
,不等式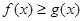 恒成立,求实数
恒成立,求实数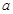 的取值范围;
的取值范围;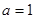 时,求最大的正整数
时,求最大的正整数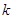 ,使得任意
,使得任意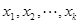
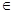
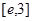 (
(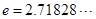 是自然对数的底数)都有
是自然对数的底数)都有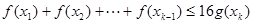 成立;
成立;
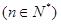 .
.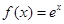 (
(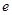 为自然对数的底数),
为自然对数的底数),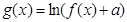 (
(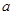 为常数),
为常数),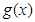 是实数集
是实数集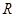 上的奇函数.
上的奇函数.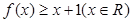 ;
; 的方程:
的方程: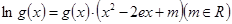 的根的个数;
的根的个数;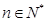 ,证明:
,证明: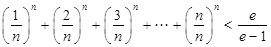 (
(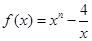 ,且
,且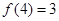 .
.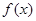 的奇偶性并说明理由;
的奇偶性并说明理由;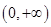 上的单调性,并证明你的结论;
上的单调性,并证明你的结论;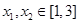 ,有
,有 成立,求
成立,求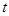 的最小值.
的最小值.