题目内容
如图,四棱锥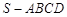 中,
中,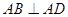 ,
, ,
,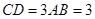 ,平面
,平面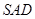 ⊥平面
⊥平面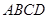 ,
,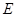 是线段
是线段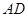 上一点,
上一点,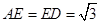 ,
,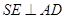 .
.
(1)证明: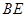 ⊥平面
⊥平面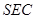 ;
;
(2)若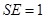 ,求直线
,求直线 与平面
与平面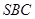 所成角的正弦值.
所成角的正弦值.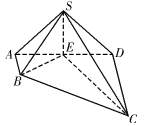
(1)证明详见解析;(2)直线 与平面
与平面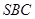 所成角的正弦值为
所成角的正弦值为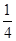 .
.
解析试题分析:(1)要证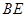 ⊥平面
⊥平面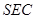 ,只须证明
,只须证明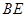 与平面
与平面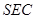 内的两条相交直线
内的两条相交直线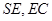 垂直即可,对于
垂直即可,对于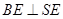 的证明,只需要根据题中面面垂直的性质及线面垂直的性质即可得出,对于
的证明,只需要根据题中面面垂直的性质及线面垂直的性质即可得出,对于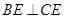 的证明,这需要在平面的直角梯形
的证明,这需要在平面的直角梯形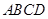 中根据
中根据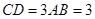 及
及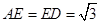 得出
得出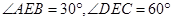 ,进而可得出
,进而可得出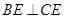 ,问题得以证明;(2)分别以
,问题得以证明;(2)分别以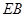 、
、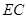 、
、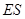 所在的直线为
所在的直线为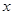 、
、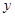 、
、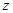 轴建立空间直角坐标系,进而写出有效点的坐标,设平面
轴建立空间直角坐标系,进而写出有效点的坐标,设平面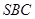 的法向量
的法向量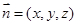 ,由
,由 确定该法向量的一个坐标,进而根据线面角的向量计算公式
确定该法向量的一个坐标,进而根据线面角的向量计算公式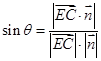 即可得出直线
即可得出直线 与平面
与平面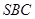 所成角的正弦值.
所成角的正弦值.
(1)证明:由已知条件可知:在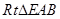 中,
中,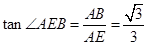 ,所以
,所以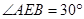
在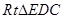 中,
中,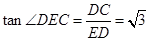 ,所以
,所以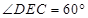
所以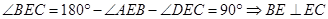 ……①
……①
又因平面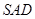 ⊥平面
⊥平面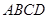 ,
,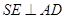
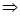
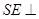 面
面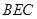
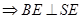 ……②
……②
由①②及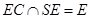 可得
可得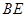 ⊥平面
⊥平面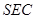
(2)如图分别以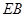 、
、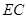 、
、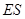 所在的直线为
所在的直线为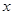 、
、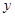 、
、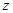 轴建立空间直角坐标系
轴建立空间直角坐标系
则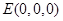 ,
,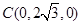 ,
,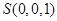 ,
,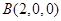
所以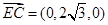 ,
,
设平面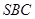 的法向量
的法向量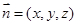 ,则有:
,则有: 即
即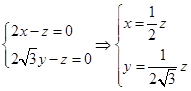 ,取
,取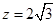 ,则
,则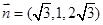
设直线直线 与平面
与平面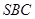 所成角为
所成角为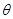 ,有
,有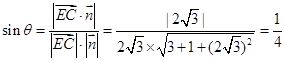
所以直线 与平面
与平面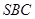 所成角的正弦值为
所成角的正弦值为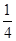 .
.
考点:1.空间中的垂直关系;2.空间向量在解决空间角中的应用.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
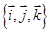 为单位正交基,且
为单位正交基,且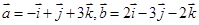 ,则向量
,则向量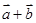 与向量
与向量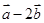 的坐标分别是______________;_________________.
的坐标分别是______________;_________________.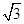 ,E是PB上任意一点.
,E是PB上任意一点.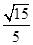 ,若E为PB的中点,求EC与平面PAB所成角的正弦值.
,若E为PB的中点,求EC与平面PAB所成角的正弦值.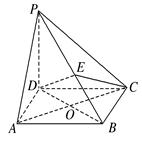
 中,
中, 分别是棱
分别是棱 的中点,点
的中点,点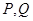 分别在棱
分别在棱 ,
,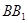 上移动,且
上移动,且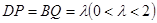 .
. 时,证明:直线
时,证明:直线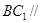 平面
平面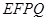 ;
; ,使平面
,使平面 所成的二面角为直二面角?若存在,求出
所成的二面角为直二面角?若存在,求出
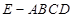 中,平面
中,平面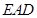
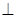 平面
平面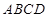 ,
,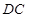 //
//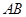 ,
,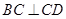 ,
,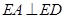 ,且
,且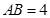 ,
,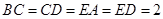 .
.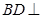 平面
平面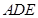 ;
;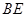 和平面
和平面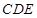 所成角的正弦值;
所成角的正弦值; 上是否存在一点
上是否存在一点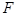 使得平面
使得平面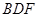
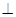 平面
平面
 中,底面
中,底面 是直角梯形,
是直角梯形, ,
, ,
,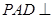 平面
平面
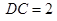 ,
,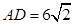 ,
, ,
, ,且
,且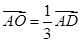 .
.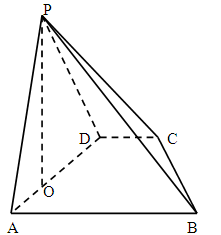
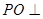 平面
平面 与平面
与平面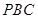 所成二面角的大小为
所成二面角的大小为 ,求
,求 的值.
的值.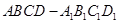 中,底面ABCD是边长为1的正方形,E为
中,底面ABCD是边长为1的正方形,E为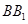 延长线上的一点且满足
延长线上的一点且满足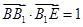 .
.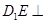 平面
平面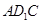 ;
;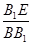 为何值时,二面角
为何值时,二面角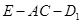 的大小为
的大小为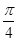 .
.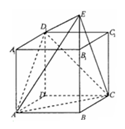
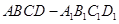 中,P是侧棱
中,P是侧棱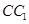 上的一点,
上的一点,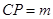 .
. 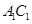 上是否存在一个定点
上是否存在一个定点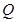 ,使得对任意的m,
,使得对任意的m,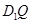 ⊥AP,并证明你的结论.
⊥AP,并证明你的结论. 
 中,
中, 为
为 的中点,
的中点, ,
, ,
, .将此平面四边形
.将此平面四边形 折成直二面角
折成直二面角 ,
,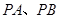 ,设
,设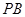 中点为
中点为 .
.
 平面
平面 ;
; 上是否存在一点
上是否存在一点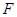 ,使得
,使得 平面
平面 与平面
与平面