题目内容
双曲线
思路解析:判断轨迹形状,得解法一;点M是被动点,P是主动点且在已知曲线上得解法二相关点法(中间变量法). 解法一:(待定系数法)如图所示. ∵M是△PF1F2的重心,∴|OM|= 过M作MA∥PF1交x轴于A,过M作MB∥PF2交x轴于B.∴|PF1|=3|MA|,|PF2|=3|MB|. ∵P在双曲线上, ∴||PF1|-|PF2||=2a=6. ∴|3|MA|-3|MB||=6. ∴||MA|-|MB||=2< ∴点M是以A、B为焦点的双曲线,设其标准方程是 则2a=2,2c=|AB|= ∴a2=1,b2=c2-a2=( ∴点M的轨迹方程是x2- 解法二:(相关点法)设M(x,y),P(x0,y0). ∵M是△PF1F2的重心, ∴M分 ∴ ∵P在双曲线上, ∴ ∴点M在轨迹方程是x2- 深化升华 当动点M随点P变化而变化时,点P在已知曲线上,求动点M的轨迹方程,常利用相关点法(中间变量代入法).当题目中出现重心时,常用重心的性质:到顶点距离是到对边中点距离的二倍;三角形重心坐标公式.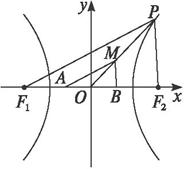
![]() |OP|.
|OP|.![]()
![]() =|AB|.
=|AB|.![]() -
-![]() =1(a>0,b>0).
=1(a>0,b>0).![]()
![]() .
.![]() )2-1=
)2-1=![]() .
.![]() =1(y≠0).
=1(y≠0).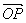 的比λ=
的比λ=![]() .
.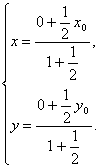 解得
解得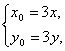 即P(3x,3y).
即P(3x,3y).![]() -(3y)2=1.
-(3y)2=1.![]() =1(y≠0).
=1(y≠0).

课课练与单元测试系列答案
世纪金榜小博士单元期末一卷通系列答案
单元测试AB卷台海出版社系列答案
黄冈新思维培优考王单元加期末卷系列答案
名校名师夺冠金卷系列答案
小学英语课时练系列答案
培优新帮手系列答案


课堂作业广西教育出版社系列答案
 与双曲线
与双曲线 -y2=1有公共焦点,且离心率为
-y2=1有公共焦点,且离心率为 .A,B分别是椭圆C的左顶点和右顶点.点S是椭圆C上位于x轴上方的动点.直线AS,BS分别与直线l:x=
.A,B分别是椭圆C的左顶点和右顶点.点S是椭圆C上位于x轴上方的动点.直线AS,BS分别与直线l:x= 分别交于M,N两点.
分别交于M,N两点. ?若存在确定点T的个数,若不存在,说明理由.
?若存在确定点T的个数,若不存在,说明理由.
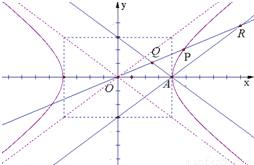
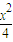 -y2=1的右顶点为A,P是双曲线上异于顶点的一个动点,从A引双曲线的两条渐近线的平行线与直线OP (O为坐标原点)分别交于Q和R两点.
-y2=1的右顶点为A,P是双曲线上异于顶点的一个动点,从A引双曲线的两条渐近线的平行线与直线OP (O为坐标原点)分别交于Q和R两点.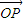 |2=|
|2=|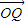 •
•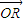 |;
|;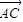 =
= (
(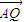 +
+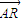 ),求点C的轨迹方程.
),求点C的轨迹方程.