题目内容
已知ax=(6-a)2y=3(1<a<5),则
+
的最大值为( )
| 2 |
| x |
| 1 |
| y |
分析:由ax=(6-a)2y=3(1<a<5),可求得
=log3a,
=log3(6-a),于是可得
+
=log3a2+log3(6-a)2=log3(6-a)2•a2,利用基本不等式即可.
| 1 |
| x |
| 1 |
| 2y |
| 2 |
| x |
| 1 |
| y |
解答:解:∵ax=(6-a)2y=3(1<a<5),
∴
=log3a,
=log3(6-a),
∴
+
=log3a2+log3(6-a)2=log3(6-a)2•a2,
∵1<a<5,
∴(6-a)2•a2=(6-a)•(6-a)•a•a≤[
]4=34(当且仅当6-a=a,即a=3时取“=”).
∴log3(6-a)2•a2≤log334=4.
故选C.
∴
| 1 |
| x |
| 1 |
| 2y |
∴
| 2 |
| x |
| 1 |
| y |
∵1<a<5,
∴(6-a)2•a2=(6-a)•(6-a)•a•a≤[
| (6-a)+(6-a)+a+a |
| 4 |
∴log3(6-a)2•a2≤log334=4.
故选C.
点评:本题考查指数式与对数式的互化,着重考查基本不等式的应用,求得得
+
=log3(6-a)2•a2应用基本不等式的关键,属于中档题.
| 2 |
| x |
| 1 |
| y |

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
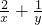 的最大值为
的最大值为 的最大值为( )
的最大值为( ) 的最大值为
的最大值为