题目内容
设点P在曲线 上,点Q在曲线y=ln(2x)上,则|PQ|最小值为( )
上,点Q在曲线y=ln(2x)上,则|PQ|最小值为( )A.1-ln2
B.

C.1+ln2
D.

【答案】分析:由于函数 与函数y=ln(2x)互为反函数,图象关于y=x对称,要求|PQ|的最小值,只要求出函数
与函数y=ln(2x)互为反函数,图象关于y=x对称,要求|PQ|的最小值,只要求出函数 上的点
上的点 到直线y=x的距离为
到直线y=x的距离为 的最小值,
的最小值,
设g(x)= ,利用导数可求函数g(x)的单调性,进而可求g(x)的最小值,即可求
,利用导数可求函数g(x)的单调性,进而可求g(x)的最小值,即可求
解答:解:∵函数 与函数y=ln(2x)互为反函数,图象关于y=x对称
与函数y=ln(2x)互为反函数,图象关于y=x对称
函数 上的点
上的点 到直线y=x的距离为
到直线y=x的距离为
设g(x)= ,(x>0)则
,(x>0)则
由 ≥0可得x≥ln2,
≥0可得x≥ln2,
由 <0可得0<x<ln2
<0可得0<x<ln2
∴函数g(x)在(0,ln2)单调递减,在[ln2,+∞)单调递增
∴当x=ln2时,函数g(x)min=1-ln2

由图象关于y=x对称得:|PQ|最小值为
故选B
点评:本题主要考查了点到直线的距离公式的应用,注意本题解法中的转化思想的应用,根据互为反函数的对称性把所求的点点距离转化为点线距离,构造很好
 与函数y=ln(2x)互为反函数,图象关于y=x对称,要求|PQ|的最小值,只要求出函数
与函数y=ln(2x)互为反函数,图象关于y=x对称,要求|PQ|的最小值,只要求出函数 上的点
上的点 到直线y=x的距离为
到直线y=x的距离为 的最小值,
的最小值,设g(x)=
 ,利用导数可求函数g(x)的单调性,进而可求g(x)的最小值,即可求
,利用导数可求函数g(x)的单调性,进而可求g(x)的最小值,即可求解答:解:∵函数
 与函数y=ln(2x)互为反函数,图象关于y=x对称
与函数y=ln(2x)互为反函数,图象关于y=x对称函数
 上的点
上的点 到直线y=x的距离为
到直线y=x的距离为
设g(x)=
 ,(x>0)则
,(x>0)则
由
 ≥0可得x≥ln2,
≥0可得x≥ln2,由
 <0可得0<x<ln2
<0可得0<x<ln2∴函数g(x)在(0,ln2)单调递减,在[ln2,+∞)单调递增
∴当x=ln2时,函数g(x)min=1-ln2

由图象关于y=x对称得:|PQ|最小值为

故选B
点评:本题主要考查了点到直线的距离公式的应用,注意本题解法中的转化思想的应用,根据互为反函数的对称性把所求的点点距离转化为点线距离,构造很好

练习册系列答案
相关题目
 上,点Q在曲线
上,点Q在曲线 上,求|
上,求| |的最小值.
|的最小值. 上,点Q在曲线
上,点Q在曲线 上,则|PQ|最小值为(
)
上,则|PQ|最小值为(
) B.
B.  C.
C.
 D.
D.

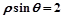 上,点Q在曲线
上,点Q在曲线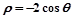 上,求|
上,求|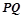 |的最小值.
|的最小值.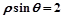 上,点Q在曲线
上,点Q在曲线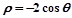 上,求|
上,求|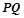 |的最小值.
|的最小值.