题目内容
(本题满分16分）
已知函数
且
.
（1）求
的单调递增区间；
（2）若函数
与函数在
时有相同的值域，求
的值；
（3）设
，函数
，若对于任意
，总存在
，使得
成立，求的取值范围。
(本题满分16分）
解: （1）
，
易得
的单调递增区间为
。…5分
（2）∵在
上单调递减，∴其值域为
，即，
。
∵
为最大值，∴最小值只能为
或
，
若
；若
。
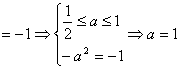综上得
。 ……………10分
（3）设
的值域为
,由题意知，
。以下先证的单调性：设
，
∵
，
（
，
），
∴在
上单调递减。
∴
，
∴
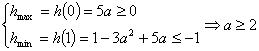的取值范围是
。 ……………16分
注：第(1)、（3）问也可用导数求解.
练习册系列答案
课时训练江苏人民出版社系列答案
相关题目
（
，
、
是常数，且
），对定义域内任意
（
且
），恒有
成立．
的解析式，并写出函数的定义域；
．
的前
项和为
，且
．数列
中，
，
．（1）求数列
使数列
是等比数列，求数列
；②
．
在
上的单调性；
，使
，则称
的不动点，现已知该函数有且仅有一个不动点，求
的值；
在