题目内容

4．若函数y=loga（1+2x+3x+m）的值域为R，那么实数m的取值范围为（-∞，-1]．

分析 若函数y=loga（1+2x+3x+m）的值域为R，则1+2x+3x+m可以为任意正数，进而得到答案．

解答 解：若函数y=loga（1+2x+3x+m）的值域为R，
则1+2x+3x+m可以为任意正数，
即函数y=1+2x+3x+m的值域包含（0，+∞），
即m+1≤0，
解得：m∈（-∞，-1]，
故答案为：（-∞，-1]

点评 本题考查的知识点是对数函数的图象和性质，熟练掌握对数函数的图象和性质，是解答的关键．

练习册系列答案
相关题目
11．计算：
（1）1og520-1og54；
（2）1og3（27×92）；
（3）1g1002-1og${\;}_{\frac{1}{3}}$$\frac{1}{81}$
（4）lg0.0001+1ne-1og8.31．
12．把集合A={x|-1≤x≤5，x∈Z}，用列举法表示为{-1，0，1，2，3，4，5}．
9．已知△ABC的顶点坐标为A（2，1），B（-2，3），C（0，-1），求BC边上的高所在的直线的方程．
16．某皮鞋厂从今年1月份开始投产，并且前4个月的产量分别为如表所示
月份1234
产量（万双）1.021.101.161.18
由于产品质量好，款式新颖，前几个月的产品销售情况良好，为了推销员在推销产品时，按受订单不至于过多或过少，需要估测以后几个月的产量，厂里分析，产量的增加是由于工人生产熟练和理顺了生产流程，厂里也暂时不准备增加设备和工人．如果用x表示月份，用y表示产量，试比较y=a$\sqrt{x}$+b和y=abx+c哪一个更好些？（函数模型y=a$\sqrt{x}$+b，要求用第1、4月份的数据确定a、b，函数模型y=abx+c要求用第1、2、3月份的数据确定a、b、c，精确到0.01，$\sqrt{2}≈1.414$，$\sqrt{3}≈1.732$）
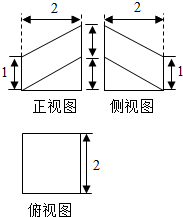9．某几何体的三视图如图所示，求该几何体的体积．
16．函数f（x）=loga（x+$\sqrt{3}$）+loga（x-$\sqrt{3}$）的图象过定点P，则点P的坐标为（2，0）．
13．（1）在椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1中，过左焦点F1作x轴的垂线交椭圆于点N，若∠F1NF2=60°．求椭圆的离心率；
（2）双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的两个焦点为F1、F2．O为坐标原点，若在双曲线上存在一点M，使得|OM|=2a，且∠F1MF2=60°，求双曲线的渐进线方程及离心率；
（3）已知F是双曲线$\frac{{x}^{2}}{4}-\frac{{y}^{2}}{12}$=1的左焦点，点A（1，4），点P是双曲线右支上的动点，求|PF|+|PA|的最小值；
（4）抛物线y2=4x的焦点为F，准线为L，经过点F且斜率为$\sqrt{3}$的直线与抛物线在x轴上方的部分相交于点A，AK⊥l，垂足为K，求△AKF的面积．
14．已知命题p：存在x∈（-∞，1）使得x2-4x+m=0成立，命题q：方程$\frac{{x}^{2}}{{m}^{2}}$+$\frac{{y}^{2}}{2m+8}$=1表示焦点在x轴上的椭圆．
（1）若p是真命题，求实数m的取值范围；
（2）若p或q是假命题，求实数m的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网