题目内容
11.等差数列{an}中,已知a1=1,a2+a3+a5=17.(1)求数列{an}的通项公式;
(2)若数列{an}的前n项和为Sn,求Sn.
分析 (1)由通项公式可得公差为d的方程,解方程可得;
(2)把(1)的数据代入求和公式计算可得.
解答 解:(1)设等差数列{an}的公差为d,
∵a1=1,a2+a3+a5=17,
∴a2+a3+a5=3+7d=17,解得d=2,
∴数列{an}的通项公式an=1+2(n-1)2n-1;
(2)由(1)可得Sn=$\frac{n(1+2n-1)}{2}$=n2.
点评 本题考查等差数列的求和公式和通项公式,属基础题.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
3.下列几何体中,轴截面为等腰三角形的是( )
| A. | 圆柱 | B. | 圆锥 | C. | 四棱柱 | D. | 球 |
1.在数列{an}中,a1=1,Sn+1=4an+2,则a2013的值为( )
| A. | 3019×22012 | B. | 3019×22013 | C. | 3018×22012 | D. | 无法确定 |
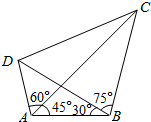 如图,在平面四边形ABCD中,AB=5$\sqrt{2}$,∠CBD=75°,∠ABD=30°,∠CAB=45°,∠CAD=60°.
如图,在平面四边形ABCD中,AB=5$\sqrt{2}$,∠CBD=75°,∠ABD=30°,∠CAB=45°,∠CAD=60°.