题目内容
15.设x为正数,当x取什么值时,函数y=$\frac{{x}^{2}+4}{x}$有最小值?最小值是多少?分析 利用${a}^{2}+{b}^{2}≥2\sqrt{ab}$即得结论.
解答 解:由题可知y=y=$\frac{{x}^{2}+4}{x}$=x+$\frac{4}{x}$≥2$\sqrt{x•\frac{4}{x}}$=4,
当且仅当x=$\frac{4}{x}$即x=2时取等号,
∴当x=2时函数y=$\frac{{x}^{2}+4}{x}$有最小值4.
点评 本题考查函数的最值,利用基本不等式是解决本题的关键,注意解题方法的积累,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
y关于x的线性回归方程$\widehat{y}$=$\widehat{a}x+\widehat{b}$为$\hat{y}$=0.7x+1.05.
| 零件的个数x(个) | 2 | 3 | 4 | 5 |
| 加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
20.sin(θ+75°)+cos(θ+45°)-$\sqrt{3}$cos(θ+15°)=( )
| A. | ±1 | B. | 1 | C. | -1 | D. | 0 |
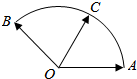 给定两个长度为1的平面向量$\overrightarrow{OA}$和$\overrightarrow{OB}$,它们的夹角为120°如图所示,点C在以O为圆心的圆弧$\overrightarrow{AB}$上变动.若$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,其中x,y∈R,则x+y的最大值是( )
给定两个长度为1的平面向量$\overrightarrow{OA}$和$\overrightarrow{OB}$,它们的夹角为120°如图所示,点C在以O为圆心的圆弧$\overrightarrow{AB}$上变动.若$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,其中x,y∈R,则x+y的最大值是( )