题目内容

过点P(2,-2)作直线交椭圆=1于A,B两点,求AB中点M的轨迹方程.

解:设M(x0,y0),直线的倾斜角为α,则直线的参数方程为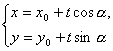(t为参数).

代入椭圆方程16(x0+tcosα)2+25(y0+tsinα)2-16×25=0(16cos2α+25sin2α)t2+

(32cosα·x0+50sinα·y0)t+16x02+25y02-16×25=0,由于(x0,y0)为中点,

∴t1+t2=0,即32x0cosα+50y0sinα=032x0+50y0·=0,

k=.

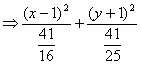代入32x0+50y0·=032(x-1)2+50(y+1)2=82=1.

练习册系列答案
相关题目
过点P（a，b）作两条直线l1，l2，斜率分别为1，-1，已知l1与圆O1：(x+2)2+(y-2)2=2交于不同的两点A，B，l2与圆O2：(x-3)2+(y-4)2=2交于不同的两点C，D，且|AB|=|CD|．
（Ⅰ）求：a，b所满足的约束条件；
（Ⅱ）求：
a2-b2a2+b2
的取值范围．
过点P(-2,0)作直线l交圆x2+y2=1于A、B两点,则|PA|·|PB|=_____________.

过点P(-2,-3)作圆C:(x-4)2+(y-2)2=9的两条切线,切点分别为A、B.求:

(1)经过圆心C,切点A、B这三点的圆的方程;

(2)直线AB的方程;

(3)线段AB的长.
过点P(2,2)作直线l被两平行线x+y+1=0,x+y-1=0截得的线段长为2,求l的方程.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网