Question

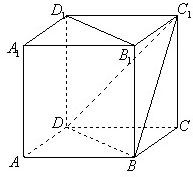
如图，在正方体ABCD-A₁B₁C₁D₁中，二面角C₁-BD-C的正切值为（　　）

• A、

  2

  2

• B、

  2

• C、

  3

• D、

  3

  3

Answer 1

分析：取BD中点E，连接CE，C₁E，根据三垂线定理易得，∠C₁EC即为所求二面角C₁-BD-C的平面角，解△C₁EC即可求出二面角C₁-BD-C的正切值．

解答：解：取BD中点E，连接CE，C₁E，
则∠C₁EC即为所求二面角C₁-BD-C的平面角
设正方体ABCD-A₁B₁C₁D₁的棱长为1，
在△C₁EC中，CC₁=1，CE=

2

2

∴tan∠C₁EC=

2

故选B

点评：本题考查的知识点是二面角的平面角及求法，其中求出二面角的平面角，将问题转化为解三角形问题是解答本题的关键．