题目内容
如图,双曲线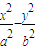 =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为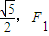 、F2分别为左、右焦点,M为左准线与渐近线在第二象限内的交点,且
、F2分别为左、右焦点,M为左准线与渐近线在第二象限内的交点,且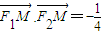 .
.(I)求双曲线的方程;
(II)设A(m,0)和
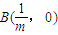 (0<m<1)是x轴上的两点.过点A作斜率不为0的直线l,使得l交双曲线于C、D两点,作直线BC交双曲线于另一点E.证明直线DE垂直于x轴.中心O为圆心,分别以a和b为半径作大圆和.
(0<m<1)是x轴上的两点.过点A作斜率不为0的直线l,使得l交双曲线于C、D两点,作直线BC交双曲线于另一点E.证明直线DE垂直于x轴.中心O为圆心,分别以a和b为半径作大圆和.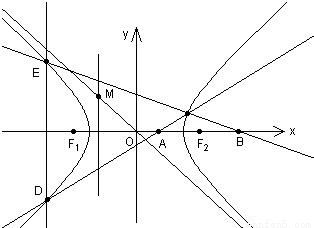
【答案】分析:(I)设点M(x,y),根据题设条件联立方程求得M的坐标,根据 求得a,b和c的关系利用a2+b2=c2求得c,b和a,答案可得.
求得a,b和c的关系利用a2+b2=c2求得c,b和a,答案可得.
(II)设点C(x1,y1),D(x2,y2),E(x3,y3),则可表示出直线l的方程,直线与双曲线联立方程,可求得x1x2的表达式,求得x2的表达式,同理可求得x3的表达式,最后得出以x2=x3,判断出故直线DE垂直于x轴.
解答:(I)解:根据题设条件,F1(-c,0),F2(c,0).
设点M(x,y),则x、y满足
因 ,解得
,解得 ,
,
故 =
=
利用a2+b2=c2,得 ,于是
,于是
因此,所求双曲线方程为x2-4y2=1.
(II)解:设点C(x1,y1),D(x2,y2),E(x3,y3),则直线l的方程为
于是C(x1,y1)、D(x2,y2)两点坐标满足
将①代入②得(x12-2x1m+m2-4y12)x2+8my12x-4y12m2-x12+2mx1-m2=0.
由已知,显然m2-2x1m+1≠0.于是
因为x1≠0,得
同理,C(x1,y1)、E(x3,y3)两点坐标满足
可解得
所以x2=x3,故直线DE垂直于x轴.
点评:本小题主要考查双曲线的标准方程和几何性质、直线方程、平面向量、曲线和方程的关系等解析几何的基础知识和基本思想方法,考查推理及运算能力.
 求得a,b和c的关系利用a2+b2=c2求得c,b和a,答案可得.
求得a,b和c的关系利用a2+b2=c2求得c,b和a,答案可得.(II)设点C(x1,y1),D(x2,y2),E(x3,y3),则可表示出直线l的方程,直线与双曲线联立方程,可求得x1x2的表达式,求得x2的表达式,同理可求得x3的表达式,最后得出以x2=x3,判断出故直线DE垂直于x轴.
解答:(I)解:根据题设条件,F1(-c,0),F2(c,0).
设点M(x,y),则x、y满足

因
 ,解得
,解得 ,
,故
 =
=
利用a2+b2=c2,得
 ,于是
,于是
因此,所求双曲线方程为x2-4y2=1.
(II)解:设点C(x1,y1),D(x2,y2),E(x3,y3),则直线l的方程为

于是C(x1,y1)、D(x2,y2)两点坐标满足

将①代入②得(x12-2x1m+m2-4y12)x2+8my12x-4y12m2-x12+2mx1-m2=0.
由已知,显然m2-2x1m+1≠0.于是

因为x1≠0,得

同理,C(x1,y1)、E(x3,y3)两点坐标满足

可解得

所以x2=x3,故直线DE垂直于x轴.
点评:本小题主要考查双曲线的标准方程和几何性质、直线方程、平面向量、曲线和方程的关系等解析几何的基础知识和基本思想方法,考查推理及运算能力.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
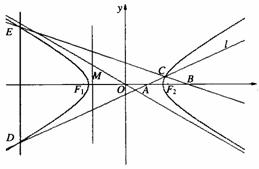
 =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为 、F2分别为左、右焦点,M为左准线与渐近线在第二象限内的交点,且
、F2分别为左、右焦点,M为左准线与渐近线在第二象限内的交点,且 .
. (0<m<1)是x轴上的两点.过点A作斜率不为0的直线l,使得l交双曲线于C、D两点,作直线BC交双曲线于另一点E.证明直线DE垂直于x轴.中心O为圆心,分别以a和b为半径作大圆和.
(0<m<1)是x轴上的两点.过点A作斜率不为0的直线l,使得l交双曲线于C、D两点,作直线BC交双曲线于另一点E.证明直线DE垂直于x轴.中心O为圆心,分别以a和b为半径作大圆和.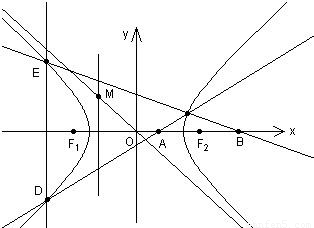
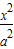 -
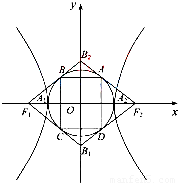
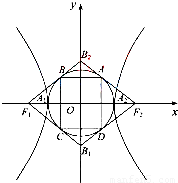
-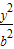 =1(a,b>0)的两顶点为A1,A2,虚轴两端点为B1,B2,两焦点为F1,F2.若以A1A2为直径的圆内切于菱形F1B1F2B2,切点分别为A,B,C,D.则:
=1(a,b>0)的两顶点为A1,A2,虚轴两端点为B1,B2,两焦点为F1,F2.若以A1A2为直径的圆内切于菱形F1B1F2B2,切点分别为A,B,C,D.则: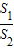 = .
= .
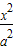 -
-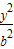 =1(a,b>0)的两顶点为A1,A2,虚轴两端点为B1,B2,两焦点为F1,F2.若以A1A2为直径的圆内切于菱形F1B1F2B2,切点分别为A,B,C,D.则:
=1(a,b>0)的两顶点为A1,A2,虚轴两端点为B1,B2,两焦点为F1,F2.若以A1A2为直径的圆内切于菱形F1B1F2B2,切点分别为A,B,C,D.则: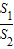 = .
= .