题目内容
已知函数 有两个零点x1,x2,则有
有两个零点x1,x2,则有
- A.x1x2=1
- B.x1x2<x1+x2
- C.x1x2=x1+x2
- D.x1x2>x1+x2
B
分析:先利用图象法确定两个零点x1,x2的取值范围,然后利用指数函数的性质进行判断.
解答: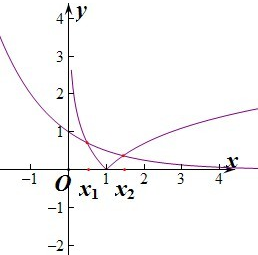 解:令
解:令 =0,得
=0,得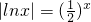 ,设函数分别为
,设函数分别为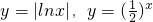 ,
,
分别在同一坐标系中,作出函数为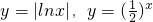 的图象,
的图象,
由图象知函数的两个零点一个大于1,一个小于1,不妨设x1<x2,则0<x1<1,x2>1.
即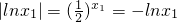 ,①,
,①,
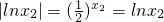 ②
②
②-①得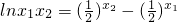 ,因为函数
,因为函数 是减函数,
是减函数,
所以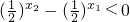 ,即lnx1x2<0,所以0<x1x2<1.
,即lnx1x2<0,所以0<x1x2<1.
所以x1x2<x1+x2.
故选B.
点评:本题考查函数零点的应用以及指数函数和对数函数的性质,综合性较强,使用数形结合思想是解决好本题的关键.
分析:先利用图象法确定两个零点x1,x2的取值范围,然后利用指数函数的性质进行判断.
解答:
 解:令
解:令 =0,得
=0,得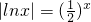 ,设函数分别为
,设函数分别为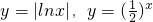 ,
,分别在同一坐标系中,作出函数为
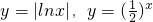 的图象,
的图象,由图象知函数的两个零点一个大于1,一个小于1,不妨设x1<x2,则0<x1<1,x2>1.
即
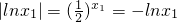 ,①,
,①,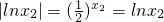 ②
②②-①得
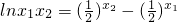 ,因为函数
,因为函数 是减函数,
是减函数,所以
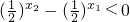 ,即lnx1x2<0,所以0<x1x2<1.
,即lnx1x2<0,所以0<x1x2<1.所以x1x2<x1+x2.
故选B.
点评:本题考查函数零点的应用以及指数函数和对数函数的性质,综合性较强,使用数形结合思想是解决好本题的关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目