Question

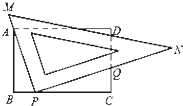如图，在矩形ABCD中，AB=4，BC=6，当直角三角板MPN 的直角顶点P在BC边上移动时，直角边MP始终经过点A，设直角三角板的另一直角边PN与CD相交于点Q．BP=x，CQ=y，那么y与x之间的函数图象大致是（　　）

A．

B．

C．

D．

Answer 1

分析：由于直角边MP始终经过点A，△APQ为直角三角形，运用勾股定理列出y与x之间的函数关系式即可．

解答：解：设BP=x，CQ=y，则AP²=4²+x²，PQ²=（6-x）²+y²，AQ²=（4-y）²+6²；
∵△APQ为直角三角形，
∴AP²+PQ²=AQ²，即4²+x²+（6-x）²+y²=（4-y）²+6²，化简得：y=-

1

4

x2+

3

2

x
整理得：y=-

1

4

（x-3）²+

9

4

根据函数关系式可看出D中的函数图象与之对应．
故选：D．

点评：本题考查的是动点变化时，两线段对应的变化关系，重点是找出等量关系，即直角三角形中的勾股定理．