题目内容
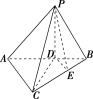
【题目】在直角坐标系
中，圆
的方程为
.
（1）若圆上有两点
，
关于直线
对称，且
，求直线
的方程；
（2）圆与
轴相交于
，
两点，圆内的动点
使
，
，
成等比数列，求
的取值范围.
【答案】（1）
，
；（2）
.
【解析】
（1）根据
，
关于直线
对称，可以求出直线
的斜率，这样设出直线方程，利用圆的垂径定理、点到直线的距离公式，可以求出直线的方程；
（2）求出
，
两点坐标，设
，由等比数列的性质，可得等式，最后求出
的表达式，再根据点在圆内，最后求出的取值范围.
（1）因为直线的斜率为
，所以直线的斜率为2，设直线的方程为：
，因为
的半径为2，
，所以圆心到直线的距离为：
，因此有：
，所以
：，.
（2）易知
，
.设，由
，
，
成等比数列，得
，两边平方得
，即
.
∴
.
由于点
在圆
内，∴
.又，∴
，得
.
∴的取值范围为.
考前必练系列答案【题目】某公司为了解某产品的获利情况，将今年1至7月份的销售收入
（单位：万元）与纯利润
（单位：万元）的数据进行整理后，得到如下表格：
月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
销售收入 | 13 | 13.5 | 13.8 | 14 | 14.2 | 14.5 | 15 |
纯利润 | 3.2 | 3.8 | 4 | 4.2 | 4.5 | 5 | 5.5 |
该公司先从这7组数据中选取5组数据求纯利润关于销售收入的线性回归方程，再用剩下的2组数据进行检验.假设选取的是2月至6月的数据.
（1）求纯利润关于销售收入
（2）若由线性回归方程得到的估计数据与检验数据的误差均不超过0.1万元，则认为得到的线性回归方程是理想的.试问该公司所得线性回归方程是否理想？
参考公式：
，
，
，
；参考数据：
.
【题目】某网络平台从购买该平台某课程的客户中，随机抽取了100位客户的数据，并将这100个数据按学时数，客户性别等进行统计，整理得到如表：
学时数 |
|
|
|
|
|
|
|
男性 | 18 | 12 | 9 | 9 | 6 | 4 | 2 |
女性 | 2 | 4 | 8 | 2 | 7 | 13 | 4 |
（1）根据上表估计男性客户购买该课程学时数的平均值（同一组中的数据用该组区间的中点值作代表，结果保留小数点后两位）；
（2）从这100位客户中，对购买该课程学时数在20以下的女性客户按照分层抽样的方式随机抽取7人，再从这7人中随机抽取2人，求这2人购买的学时数都不低于15的概率．
（3）将购买该课程达到25学时及以上者视为“十分爱好该课程者”，25学时以下者视，为“非十分爱好该课程者”．请根据已知条件完成以下
列联表，并判断是否有99．9%的把握认为“十分爱好该课程者”与性别有关？
非十分爱好该课程者 | 十分爱好该课程者 | 合计 | |
男性 | |||
女性 | |||
合计 | 100 |
附：
，
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
【题目】参加衡水中学数学选修课的同学，对某公司的一种产品销量与价格进行统计，得到如下数据和散点图：
定价 |
|
|
|
|
|
|
年销售 |
|
|
|
|
|
|
|
|
|
|
|
|
|
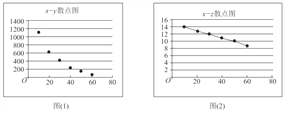
（参考数据：
）
（I）根据散点图判断，
与
，
与哪一对具有较强的线性相关性（给出判断即可，不必说明理由）？
（II）根据（I）的判断结果有数据，建立关于的回归方程（方程中的系数均保留两位有效数字）；
（III）定价为多少元/
时，年利润的预报值最大？
附：对一组数据
，其回归直线
的斜率和截距的最小二乘估计分别为：
.
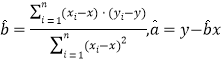【题目】某地区不同身高
的未成年男性的体重平均值
如下表：
身高x（cm） | 60 | 70 | 80 | 90 | 100 | 110 | 120 | 130 | 140 |
体重y(kg) | 6.13 | 7.90 | 9.99 | 12.15 | 15.02 | 17.50 | 20.92 | 26.86 | 31.11 |
已知
与
之间存在很强的线性相关性，
（Ⅰ）据此建立
与之间的回归方程；
（Ⅱ）若体重超过相同身高男性体重平均值的
倍为偏胖，低于
倍为偏瘦，那么这个地区一名身高
体重为
的在校男生的体重是否正常？
参考数据：
附：对于一组数据
，其回归直线
中的斜率和截距的最小二乘估计分别为
