题目内容
【题目】![]() 不是直角三角形,它的三个角
不是直角三角形,它的三个角![]() 所对的边分别为
所对的边分别为![]() ,已知
,已知![]() .
.
(1)求证: ![]() ;
;
(2)如果![]() ,求
,求![]() 面积的最大值.
面积的最大值.
【答案】(1)见解析;(2)48
【解析】试题分析:(1)由![]() ,根据正弦定理及两角和的正弦公式化简可得
,根据正弦定理及两角和的正弦公式化简可得![]() ,因为
,因为![]() 不是直角三角形,所以
不是直角三角形,所以![]() ,由正弦定理可得
,由正弦定理可得![]() ;(2)视
;(2)视![]() 为定点,求出满足
为定点,求出满足![]() 条件下
条件下![]() 的轨迹为一个圆,圆心在直
的轨迹为一个圆,圆心在直![]() 上,当
上,当![]() 上升到离直线
上升到离直线![]() 最远时面积最大.
最远时面积最大.
试题解析:(1)由![]() ,根据正弦定理可得
,根据正弦定理可得![]()
![]() ,
, ![]() ,因为
,因为![]() 不是直角三角形,所以
不是直角三角形,所以![]() ,由正弦定理可得
,由正弦定理可得![]() ;
;
(2)方法一:b=2a.c=12,余弦定理用a表示cosC,表示出sinC,进而用a表示出![]() ,求出该函数的最大值.(最费力的做法)
,求出该函数的最大值.(最费力的做法)
方法二:视A.B为定点,求出满足b=2a条件下C的轨迹为一个圆,圆心在直线AB上,当C上升到离直线AB最远时面积最大。
方法三:利用海伦公式直接将面积表示为a的函数
![]()
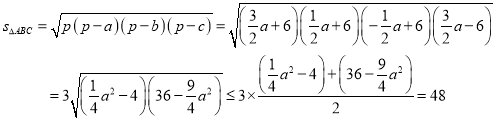
方法三为最简捷办法,凡只涉及边的面积问题可优先想到海伦公式。

练习册系列答案
相关题目
