题目内容
如图所示，圆的内接△ABC的∠C的平分线CD延长后交圆于点E，连接BE，已知BD=3，CE=7，BC=5，则线段BE=（ ）分析：先分析已知线段与未知线段之间的关系，发现他们所在的三角形相似，所以可以利用三角形相似的性质构造方程，解方程即可得到答案．
解答：解：由题知，在△BED和△BCE中，
∠EBD=∠ACE=∠CBE，∠BED=∠BCE，
∴△BED～△BCE，
所以
=
，
即
=
∴BE=
．
故选B．
∠EBD=∠ACE=∠CBE，∠BED=∠BCE，
∴△BED～△BCE，
所以
| BE |
| EC |
| BD |
| BC |
即
| BE |
| 7 |
| 3 |
| 5 |
∴BE=
| 21 |
| 5 |
故选B．
点评：求线段的长度，要先分析已知线段与未知线段之间的关系，可利用相似三角形的性质，平行线分线段成比例定理等，构造已知量与未知量之间的方程，解方程进行求解．
练习册系列答案
开心蛙口算题卡系列答案
相关题目
如图所示，圆的内接△ABC的∠C的平分线CD延长后交圆于点E，连接BE，已知BD=3，CE=7，BC=5，则线段BE=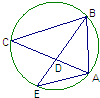
如图所示，圆的内接三角形ABC的角平分线BD与AC交于点D，与圆交于点E，连接AE，已知ED=3，BD=6，则线段AE的长=
