题目内容
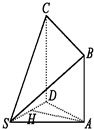
如图甲，在等边三角形ABC中，D，E分别是AB，AC边上的点，AD=AE，F是BC上的点，AF与DE交于点G，将△ABF沿AF折起，得到如图乙所示的三棱锥A-BCF，证明：DE∥平面BCF．
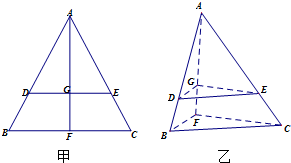
证明：∵折叠前，AD=AE，AB=AC，
=
，∴DE∥BC，
折叠后，DG∥BF，EG∥FC，
又DG，EG?平面BCF，BF，FC?平面BCF，
∴DG∥平面BCF，EG∥平面BCF，DG∩GE=G，
∴平面DEG∥平面BCF，DE?平面DEG，
∴DE∥平面BCF．
| AD |
| AB |
| AE |
| AC |
折叠后，DG∥BF，EG∥FC，
又DG，EG?平面BCF，BF，FC?平面BCF，
∴DG∥平面BCF，EG∥平面BCF，DG∩GE=G，
∴平面DEG∥平面BCF，DE?平面DEG，
∴DE∥平面BCF．
练习册系列答案
相关题目
