题目内容
在△ABC中,已知|BC|=4,BC的中点在坐标原点,点B的坐标是(-2,0),AB⊥AC,
(1)求动点A的轨迹方程;
(2)若直线l:mx-y+2m-2=0与点A的轨迹恰有一个公共点,求m的值;
(3)若(2)中m的值是函数 f(x)=x2+sinα•x+n的零点,求tan(
-α)的值.
(1)求动点A的轨迹方程;
(2)若直线l:mx-y+2m-2=0与点A的轨迹恰有一个公共点,求m的值;
(3)若(2)中m的值是函数 f(x)=x2+sinα•x+n的零点,求tan(
| 3π | 2 |
分析:(1)通过直线的垂直得到斜率的乘积是-1,化简可得动点A的轨迹方程;
(2)利用图象推出直线l:mx-y+2m-2=0与点A的轨迹恰有一个公共点,直接求m的值;
(3)通过(2)中m的值是函数 f(x)=x2+sinα•x+n的零点,通过α所在象限直接求tan(
-α)的值即可.
(2)利用图象推出直线l:mx-y+2m-2=0与点A的轨迹恰有一个公共点,直接求m的值;
(3)通过(2)中m的值是函数 f(x)=x2+sinα•x+n的零点,通过α所在象限直接求tan(
| 3π |
| 2 |
解答: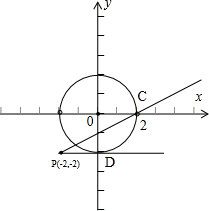 (14分)解:(1)由已知,C(2,0),设动点A的坐标为(x,y),
(14分)解:(1)由已知,C(2,0),设动点A的坐标为(x,y),
则直线AB、AC的斜率分别为kAB=
,kAC=
,
∵AB⊥AC,kAC•kAB=-1
∴
•
=-1,化简得x2+y2=4,由已知△ABC,有x≠±2,否则A、B、C共线,
∴动点的轨迹方程是:x2+y2=4(x≠±2).
(2)直线l的方程即为m(x+2)-(y+2)=0,则它经过定点P(-2,-2),
∵直线l:mx-y+2m-2=0与点A的轨迹恰有一个公共点,
∴直线l经过点C(2,0)或点D(0,-2)(如图所示)
∴m(2+2)-(0+2)=0或m(0+2)-(-2+2)=0
解得m=
或m=0…(9分)
(3)∵m的值都是函数 f(x)=x2+sinα•x+n的零点
∴
和0是方程x2+sinα•x+n=0的解
∴
+0=-sinα,故sinα=-
…(10分)
①当α是第三象限角时,cosα=-
=-
=-
,
∴tan(
-α)=tan(
-α)=
=
=
=
…(12分)
②当α是第四象限角时,cosα=
∴tan(
-α)=
=
=-
…(14分).
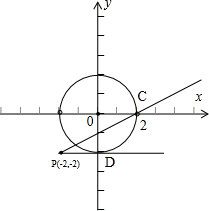 (14分)解:(1)由已知,C(2,0),设动点A的坐标为(x,y),
(14分)解:(1)由已知,C(2,0),设动点A的坐标为(x,y),则直线AB、AC的斜率分别为kAB=
| y |
| x+2 |
| y |
| x-2 |
∵AB⊥AC,kAC•kAB=-1
∴
| y |
| x+2 |
| y |
| x-2 |
∴动点的轨迹方程是:x2+y2=4(x≠±2).
(2)直线l的方程即为m(x+2)-(y+2)=0,则它经过定点P(-2,-2),
∵直线l:mx-y+2m-2=0与点A的轨迹恰有一个公共点,
∴直线l经过点C(2,0)或点D(0,-2)(如图所示)
∴m(2+2)-(0+2)=0或m(0+2)-(-2+2)=0
解得m=
| 1 |
| 2 |
(3)∵m的值都是函数 f(x)=x2+sinα•x+n的零点
∴
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
①当α是第三象限角时,cosα=-
| 1-sin2α |
1-(-
|
| ||
| 2 |
∴tan(
| 3π |
| 2 |
| π |
| 2 |
sin(
| ||
cos(
|
| cosα |
| sinα |
-
| ||||
-
|
| 3 |
②当α是第四象限角时,cosα=
| ||
| 2 |
∴tan(
| 3π |
| 2 |
| cosα |
| sinα |
| ||||
-
|
| 3 |
点评:本题考查轨迹方程的求法,数形结合以及分类讨论思想的应用,考查分析问题解决问题的能力.

练习册系列答案
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目