题目内容
设{an}是公比为正数的等比数列，若a3=4，a5=16，则数列{an}的前5项和为
- A.41
- B.15
- C.32
- D.31
D
分析：由a3=4，a5=16，可求出公比，进而得到首项，再根据前n项和公式，即可求数列的前5项和．
解答：由于a3=4，a5=16，则
，
又由{an}是公比为正数的等比数列，则q=2．
又∵a3=4，∴a1=1，
∴数列{an}的前5项和
=31．
故答案选D．
点评：本题考查了等比数列的前n项和．要求前n项和，就要知道首项和公比．而已知条件是数列的两项，故需根据通项公式联立方程组，解出首项与公比即可．
分析：由a3=4，a5=16，可求出公比，进而得到首项，再根据前n项和公式，即可求数列的前5项和．
解答：由于a3=4，a5=16，则
，又由{an}是公比为正数的等比数列，则q=2．
又∵a3=4，∴a1=1，
∴数列{an}的前5项和
=31．故答案选D．
点评：本题考查了等比数列的前n项和．要求前n项和，就要知道首项和公比．而已知条件是数列的两项，故需根据通项公式联立方程组，解出首项与公比即可．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
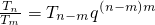（q＞0是常数）．