题目内容
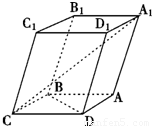
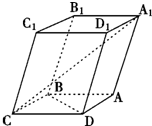 如图,一块矿石晶体的形状为四棱柱,底面ABCD是正方形,CC1=3,CD=2,且∠C1CB=∠C1CD=60°.
如图,一块矿石晶体的形状为四棱柱,底面ABCD是正方形,CC1=3,CD=2,且∠C1CB=∠C1CD=60°.
(1)设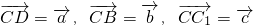 ,试用
,试用 表示
表示 ;
;
(2)O为四棱柱的中心,求CO的长;
(3)求证:A1C⊥BD.
解:(1)由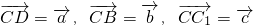 ,得
,得 .
.
所以, .
.
(2)O为四棱柱的中心,即O为线段A1C的中点.
由已知条件,得 ,
, ,
, ,
, ,
, .
.
根据向量加减法得 ,
, .
.
=22+22+32+0+2×3×2×cos60°+2×3×2×cos60°=29.
∴A1C的长为 .
.
所以 .
.
(3)∵
=22+2×3×cos60°-22-2×3×cos60°=0,
∴CA1⊥BD.
分析:(1)利用空间向量的加法,可得平行六面体的体对角线,可得 ,再利用
,再利用 与
与 互为相反向量,就可求出
互为相反向量,就可求出 .
.
(2)因为O为四棱柱的中心,所以O为线段A1C的中点,所以要求CO的长,只需求出A1C的长即可.利用(1)中所求
 ,再求模即可.
,再求模即可.
(3)要证A1C⊥BD,只需证明 =0,即可,根据
=0,即可,根据 ,
, ,也即是证明
,也即是证明 =0,再用已知计算即可.
=0,再用已知计算即可.
点评:本题考查了用空间向量判断几何中的位置关系.注意和平面向量知识相联系.
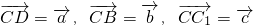 ,得
,得 .
.所以,
 .
.(2)O为四棱柱的中心,即O为线段A1C的中点.
由已知条件,得
 ,
, ,
, ,
, ,
, .
.根据向量加减法得
 ,
, .
.
=22+22+32+0+2×3×2×cos60°+2×3×2×cos60°=29.
∴A1C的长为
 .
.所以
 .
.(3)∵

=22+2×3×cos60°-22-2×3×cos60°=0,
∴CA1⊥BD.
分析:(1)利用空间向量的加法,可得平行六面体的体对角线,可得
 ,再利用
,再利用 与
与 互为相反向量,就可求出
互为相反向量,就可求出 .
.(2)因为O为四棱柱的中心,所以O为线段A1C的中点,所以要求CO的长,只需求出A1C的长即可.利用(1)中所求
 ,再求模即可.
,再求模即可.(3)要证A1C⊥BD,只需证明
 =0,即可,根据
=0,即可,根据 ,
, ,也即是证明
,也即是证明 =0,再用已知计算即可.
=0,再用已知计算即可.点评:本题考查了用空间向量判断几何中的位置关系.注意和平面向量知识相联系.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
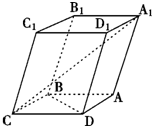 如图,一块矿石晶体的形状为四棱柱,底面ABCD是正方形,CC1=3,CD=2,且∠C1CB=∠C1CD=60°.
如图,一块矿石晶体的形状为四棱柱,底面ABCD是正方形,CC1=3,CD=2,且∠C1CB=∠C1CD=60°.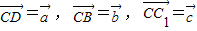 ,试用
,试用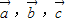 表示
表示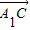 ;
;