题目内容
 的大小关系是________.
的大小关系是________.

分析:由
 =(
=( +
+ )-(2
)-(2 +
+ ),及
),及  -
- =
= -
- >0,可得
>0,可得  .
.解答:∵
 =(
=( +
+ )-(2
)-(2 +
+ ),
), -
- =2
=2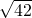 -4
-4 =
= -
- >0,
>0,∴(
 +
+ )>(2
)>(2 +
+ )>0,∴
)>0,∴ >0,
>0,∴
 .
. 故答案为:
 .
.点评:本题考查用作差比较法来比较两个实数的大小,把比较
 的大小转化为比较(
的大小转化为比较( +
+ ) 与
) 与(2
 +
+ )的大小关系,体现了转化的数学思想.
)的大小关系,体现了转化的数学思想. 
练习册系列答案
相关题目
题目内容
 的大小关系是________.
的大小关系是________.
 =(
=( +
+ )-(2
)-(2 +
+ ),及
),及  -
- =
= -
- >0,可得
>0,可得  .
. =(
=( +
+ )-(2
)-(2 +
+ ),
), -
- =2
=2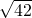 -4
-4 =
= -
- >0,
>0, +
+ )>(2
)>(2 +
+ )>0,∴
)>0,∴ >0,
>0, .
.  .
. 的大小转化为比较(
的大小转化为比较( +
+ ) 与
) 与 +
+ )的大小关系,体现了转化的数学思想.
)的大小关系,体现了转化的数学思想. 