题目内容
已知幂函数y=xn(n=-1,2,3)和椭圆C: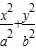 =1(a>b>0)有8个不同的交点,分别为Ai(i=1,2,…,8),F点是椭圆C的右焦点,则8条不同线段AiF(i=1,2,…,8)中所有两条线段之和最多有( )个不同的值.
=1(a>b>0)有8个不同的交点,分别为Ai(i=1,2,…,8),F点是椭圆C的右焦点,则8条不同线段AiF(i=1,2,…,8)中所有两条线段之和最多有( )个不同的值.A.28
B.25
C.24
D.20
【答案】分析:先作出图象,根据组合知识可得8条线段中所有两条线段之和有 的值,根据椭圆及幂函数的对称性可得F′A1=FA6,F′A2=FA5,F′A3=FA7,F′A4=FA8,由此可得重复值的个数.
的值,根据椭圆及幂函数的对称性可得F′A1=FA6,F′A2=FA5,F′A3=FA7,F′A4=FA8,由此可得重复值的个数.
解答:解:作出图象如图所示:
 易知y=x2关于y轴对称,y=x-1,y=x3关于原点对称,
易知y=x2关于y轴对称,y=x-1,y=x3关于原点对称,
再由椭圆的对称性可知,点A1与A6、点A3与A7、A4与A8关于原点对称,
点A2与A5关于y轴对称,
设椭圆的左焦点为F′,则F′A1=FA6,F′A2=FA5,F′A3=FA7,F′A4=FA8,
所以FA1+FA6=FA1+F′A1=2a,FA2+FA5=FA2+F′A2=2a,FA3+FA7=FA3+F′A3=2a,FA4+FA8=FA4+F′A4=2a,
所以8条不同线段AiF(i=1,2,…,8)中所有两条线段之和最多有
 =25个不同的值,
=25个不同的值,
故选B.
点评:本题考查椭圆的对称性、定义及幂函数的性质,考查数形结合思想,考查学生分析解决问题的能力.
 的值,根据椭圆及幂函数的对称性可得F′A1=FA6,F′A2=FA5,F′A3=FA7,F′A4=FA8,由此可得重复值的个数.
的值,根据椭圆及幂函数的对称性可得F′A1=FA6,F′A2=FA5,F′A3=FA7,F′A4=FA8,由此可得重复值的个数.解答:解:作出图象如图所示:
 易知y=x2关于y轴对称,y=x-1,y=x3关于原点对称,
易知y=x2关于y轴对称,y=x-1,y=x3关于原点对称,再由椭圆的对称性可知,点A1与A6、点A3与A7、A4与A8关于原点对称,
点A2与A5关于y轴对称,
设椭圆的左焦点为F′,则F′A1=FA6,F′A2=FA5,F′A3=FA7,F′A4=FA8,
所以FA1+FA6=FA1+F′A1=2a,FA2+FA5=FA2+F′A2=2a,FA3+FA7=FA3+F′A3=2a,FA4+FA8=FA4+F′A4=2a,
所以8条不同线段AiF(i=1,2,…,8)中所有两条线段之和最多有
 =25个不同的值,
=25个不同的值,故选B.
点评:本题考查椭圆的对称性、定义及幂函数的性质,考查数形结合思想,考查学生分析解决问题的能力.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
已知幂函数y=xn中的n分别为3,
,-1,则它们对应的图象依次是( )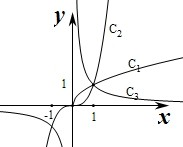
| 1 |
| 2 |

| A、C2C1C3 |
| B、C1C3C2 |
| C、C3C2C1 |
| D、C1C2C3 |
 已知幂函数y=xn在第一象限内的图象如图所示,则曲线C1、C2、C3、C4的n值可能依次为( )
已知幂函数y=xn在第一象限内的图象如图所示,则曲线C1、C2、C3、C4的n值可能依次为( )A、-2,-
| ||||
B、2,
| ||||
C、-
| ||||
D、2,
|
 已知幂函数y=xn图象如图,则n可能取的值是( )
已知幂函数y=xn图象如图,则n可能取的值是( )