题目内容
△ABC中，A、B的对边分别为a、b，a=5，b=4，且∠A=60°，那么满足条件的△ABC
- A.有一个解
- B.有两个解
- C.无解
- D.不能确定
A
分析：由A的度数求出sinA的值，再由a与b的值，利用正弦定理求出sinB的值，由sinB的值大于1及正弦函数的值域为[-1，1]，得到∠B不存在，即满足条件的三角形无解．
解答：∵a=5，b=4，且∠A=60°，
∴根据正弦定理
=
得：sinB=
=
，
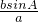∵sinB∈[-1，1]，
＜＜
，
则这样的∠B存在，B∈（45°，60°），或B∈（120°，135°），
因为∠A=60°，即满足条件的△ABC只有一个解，B∉（120°，135°），
故选A．
点评：此题属于解三角形的题型，涉及的知识有：正弦定理，特殊角的三角函数值，以及正弦函数的定义域和值域，正弦定理很好的建立了三角形的边角关系，熟练正弦定理是解本题的关键．
分析：由A的度数求出sinA的值，再由a与b的值，利用正弦定理求出sinB的值，由sinB的值大于1及正弦函数的值域为[-1，1]，得到∠B不存在，即满足条件的三角形无解．
解答：∵a=5，b=4，且∠A=60°，
∴根据正弦定理
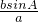=得：sinB==，∵sinB∈[-1，1]，
＜＜，则这样的∠B存在，B∈（45°，60°），或B∈（120°，135°），
因为∠A=60°，即满足条件的△ABC只有一个解，B∉（120°，135°），
故选A．
点评：此题属于解三角形的题型，涉及的知识有：正弦定理，特殊角的三角函数值，以及正弦函数的定义域和值域，正弦定理很好的建立了三角形的边角关系，熟练正弦定理是解本题的关键．
练习册系列答案
相关题目